Deep Learning (11) - CNN / CIFAR-10 / 드롭아웃
컨볼루션 신경망
CIFAR-10 살펴보기
과대적합 피하기
드롭아웃
드롭아웃(Dropout) : 과대적합을 피하기 위해 사용되는 대표적인 방법
학습이 진행되는 동안 신경망의 일부 유닛을 제외(드롭)한다.
드롭아웃 비율(Dropout Rate)은 일반적으로 0.2~0.5를 사용한다.
from keras.datasets import cifar10
from sklearn.model_selection import train_test_split
import numpy as np
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
# 기본 전처리
x_mean = np.mean(x_train, axis=(0, 1, 2))
x_std = np.std(x_train, axis=(0, 1, 2))
x_train = (x_train - x_mean) / x_std
x_test = (x_test - x_mean) / x_std
# 검증 데이터 분리
x_train, x_val, y_train, y_val = train_test_split(x_train, y_train, test_size=0.3, random_state=777)
Downloading data from https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz
170498071/170498071 [==============================] - 4s 0us/step
- 드롭아웃 사용해보기
from keras.models import Sequential
from keras.layers import Conv2D, MaxPool2D, Dense, Flatten, Dropout
from keras.optimizers import Adam
model = Sequential([
Conv2D(filters=32, kernel_size=3, padding='same', activation='relu', input_shape=(32, 32, 3)),
Conv2D(filters=32, kernel_size=3, padding='same', activation='relu'),
MaxPool2D(pool_size=(2, 2), strides=2, padding='same'),
Dropout(0.2),
Conv2D(filters=64, kernel_size=3, padding='same', activation='relu'),
Conv2D(filters=64, kernel_size=3, padding='same', activation='relu'),
MaxPool2D(pool_size=(2, 2), strides=2, padding='same'),
Dropout(0.2),
Conv2D(filters=128, kernel_size=3, padding='same', activation='relu'),
Conv2D(filters=128, kernel_size=3, padding='same', activation='relu'),
MaxPool2D(pool_size=(2, 2), strides=2, padding='same'),
Dropout(0.2),
Flatten(),
Dense(256, activation='relu'),
Dense(10, activation='softmax')
])
model.compile(optimizer=Adam(1e-4),
loss='sparse_categorical_crossentropy',
metrics=['acc'])
history = model.fit(x_train, y_train, epochs=30,
batch_size=32, validation_data=(x_val, y_val))
Epoch 1/30
1094/1094 [==============================] - 15s 7ms/step - loss: 1.7470 - acc: 0.3639 - val_loss: 1.4444 - val_acc: 0.4709
Epoch 2/30
1094/1094 [==============================] - 7s 6ms/step - loss: 1.3831 - acc: 0.4986 - val_loss: 1.2439 - val_acc: 0.5505
Epoch 3/30
1094/1094 [==============================] - 7s 6ms/step - loss: 1.2292 - acc: 0.5634 - val_loss: 1.1219 - val_acc: 0.6006
Epoch 4/30
1094/1094 [==============================] - 7s 6ms/step - loss: 1.1184 - acc: 0.6021 - val_loss: 1.0927 - val_acc: 0.6105
Epoch 5/30
1094/1094 [==============================] - 7s 6ms/step - loss: 1.0252 - acc: 0.6369 - val_loss: 1.0047 - val_acc: 0.6463
Epoch 6/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.9492 - acc: 0.6669 - val_loss: 0.9574 - val_acc: 0.6561
Epoch 7/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.8829 - acc: 0.6873 - val_loss: 0.8542 - val_acc: 0.6955
Epoch 8/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.8212 - acc: 0.7109 - val_loss: 0.8493 - val_acc: 0.7032
Epoch 9/30
1094/1094 [==============================] - 8s 7ms/step - loss: 0.7762 - acc: 0.7305 - val_loss: 0.8358 - val_acc: 0.7061
Epoch 10/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.7321 - acc: 0.7451 - val_loss: 0.7525 - val_acc: 0.7369
Epoch 11/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.6845 - acc: 0.7608 - val_loss: 0.7592 - val_acc: 0.7347
Epoch 12/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.6452 - acc: 0.7737 - val_loss: 0.7428 - val_acc: 0.7456
Epoch 13/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.6080 - acc: 0.7858 - val_loss: 0.6977 - val_acc: 0.7545
Epoch 14/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.5680 - acc: 0.8001 - val_loss: 0.7060 - val_acc: 0.7578
Epoch 15/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.5417 - acc: 0.8093 - val_loss: 0.6861 - val_acc: 0.7650
Epoch 16/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.5072 - acc: 0.8199 - val_loss: 0.6939 - val_acc: 0.7638
Epoch 17/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.4775 - acc: 0.8329 - val_loss: 0.6803 - val_acc: 0.7690
Epoch 18/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.4469 - acc: 0.8428 - val_loss: 0.7043 - val_acc: 0.7669
Epoch 19/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.4197 - acc: 0.8523 - val_loss: 0.6979 - val_acc: 0.7693
Epoch 20/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.3932 - acc: 0.8591 - val_loss: 0.7432 - val_acc: 0.7636
Epoch 21/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.3729 - acc: 0.8677 - val_loss: 0.7171 - val_acc: 0.7666
Epoch 22/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.3450 - acc: 0.8777 - val_loss: 0.7368 - val_acc: 0.7704
Epoch 23/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.3226 - acc: 0.8848 - val_loss: 0.7502 - val_acc: 0.7646
Epoch 24/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.3007 - acc: 0.8922 - val_loss: 0.7080 - val_acc: 0.7765
Epoch 25/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.2787 - acc: 0.8999 - val_loss: 0.7744 - val_acc: 0.7677
Epoch 26/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.2611 - acc: 0.9053 - val_loss: 0.7566 - val_acc: 0.7763
Epoch 27/30
1094/1094 [==============================] - 7s 7ms/step - loss: 0.2451 - acc: 0.9127 - val_loss: 0.8006 - val_acc: 0.7696
Epoch 28/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.2271 - acc: 0.9184 - val_loss: 0.7863 - val_acc: 0.7774
Epoch 29/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.2152 - acc: 0.9234 - val_loss: 0.8100 - val_acc: 0.7746
Epoch 30/30
1094/1094 [==============================] - 7s 6ms/step - loss: 0.2013 - acc: 0.9277 - val_loss: 0.8327 - val_acc: 0.7735
import matplotlib.pyplot as plt
his_dict = history.history
loss = his_dict['loss']
val_loss = his_dict['val_loss']
epochs = range(1, len(loss)+1)
fig = plt.figure(figsize=(10, 5))
# 손실 그리기
ax1 = fig.add_subplot(1, 2, 1)
ax1.plot(epochs, loss, color='blue', label='train_loss')
ax1.plot(epochs, val_loss, color='orange', label='val_loss')
ax1.set_title('train and val loss')
ax1.set_xlabel('epochs')
ax1.set_ylabel('loss')
ax1.legend()
acc = his_dict['acc']
val_acc = his_dict['val_acc']
# 정확도 그리기
ax2 = fig.add_subplot(1, 2, 2)
ax2.plot(epochs, acc, color='blue', label='train_acc')
ax2.plot(epochs, val_acc, color='orange', label='val_acc')
ax2.set_title('train and val acc')
ax2.set_xlabel('epochs')
ax2.set_ylabel('loss')
ax2.legend()
<matplotlib.legend.Legend at 0x7fcc6632c6a0>
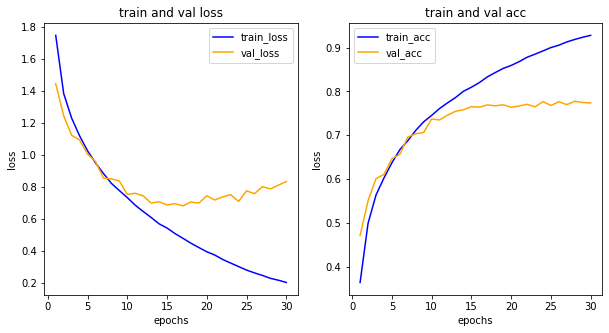
일반모델, 규제화 함수를 사용한 모델 둘에 비해 매우 강력한 과대적합 방지 기능을 보여준다.
Reference
- 이 포스트는 SeSAC 인공지능 자연어처리, 컴퓨터비전 기술을 활용한 응용 SW 개발자 양성 과정 - 심선조 강사님의 강의를 정리한 내용입니다.

댓글남기기