Deep Learning (12) - CNN / CIFAR-10 / 배치 정규화
컨볼루션 신경망
CIFAR-10 살펴보기
과대적합 피하기
배치 정규화
내부 공선성(internal Covariance Shift)을 해결하기 위해 고안되었다.
신경망층의 출력값이 가질 수 있는 범위, 출력값의 분포의 범위를 줄여주어 불확실성을 어느정도 감소시키는 방법이다.
- 장점
- 높은 학습률을 사용하여 빠른 속도로 학습 진행이 가능
- 자체적인 규제 효과가 있기에 과대적합 문제를 피할 수 있음
- 일반적인 모델 구성 순서
Dense 또는 Conv2D -> Batchnormalization() -> Activation()
from keras.datasets import cifar10
from sklearn.model_selection import train_test_split
import numpy as np
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
# 기본 전처리
x_mean = np.mean(x_train, axis=(0, 1, 2))
x_std = np.std(x_train, axis=(0, 1, 2))
x_train = (x_train - x_mean) / x_std
x_test = (x_test - x_mean) / x_std
# 검증 데이터 분리
x_train, x_val, y_train, y_val = train_test_split(x_train, y_train, test_size=0.3, random_state=777)
Downloading data from https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz
170498071/170498071 [==============================] - 4s 0us/step
- 배치 정규화 사용해보기
from keras.models import Sequential
from keras.layers import Conv2D, MaxPool2D, Dense, Flatten, Activation, BatchNormalization
from keras.optimizers import Adam
model = Sequential([
Conv2D(filters=32, kernel_size=3, padding='same', input_shape=(32, 32, 3)),
BatchNormalization(),
Activation('relu'),
Conv2D(filters=32, kernel_size=3, padding='same'),
BatchNormalization(),
Activation('relu'),
MaxPool2D(pool_size=(2, 2), strides=2, padding='same'),
Conv2D(filters=64, kernel_size=3, padding='same'),
BatchNormalization(),
Activation('relu'),
Conv2D(filters=64, kernel_size=3, padding='same'),
BatchNormalization(),
Activation('relu'),
MaxPool2D(pool_size=(2, 2), strides=2, padding='same'),
Conv2D(filters=128, kernel_size=3, padding='same'),
BatchNormalization(),
Activation('relu'),
Conv2D(filters=128, kernel_size=3, padding='same'),
BatchNormalization(),
Activation('relu'),
MaxPool2D(pool_size=(2, 2), strides=2, padding='same'),
Flatten(),
Dense(256),
BatchNormalization(),
Activation('relu'),
Dense(10, activation='softmax')
])
model.compile(optimizer=Adam(1e-4),
loss='sparse_categorical_crossentropy',
metrics=['acc'])
history = model.fit(x_train, y_train, epochs=30,
batch_size=32, validation_data=(x_val, y_val))
Epoch 1/30
1094/1094 [==============================] - 22s 11ms/step - loss: 1.4108 - acc: 0.4993 - val_loss: 1.1596 - val_acc: 0.5887
Epoch 2/30
1094/1094 [==============================] - 10s 9ms/step - loss: 0.9904 - acc: 0.6513 - val_loss: 1.0147 - val_acc: 0.6417
Epoch 3/30
1094/1094 [==============================] - 9s 9ms/step - loss: 0.7901 - acc: 0.7296 - val_loss: 0.9951 - val_acc: 0.6533
Epoch 4/30
1094/1094 [==============================] - 9s 8ms/step - loss: 0.6344 - acc: 0.7879 - val_loss: 0.9123 - val_acc: 0.6819
Epoch 5/30
1094/1094 [==============================] - 10s 9ms/step - loss: 0.5066 - acc: 0.8375 - val_loss: 0.9636 - val_acc: 0.6726
Epoch 6/30
1094/1094 [==============================] - 10s 9ms/step - loss: 0.3916 - acc: 0.8798 - val_loss: 0.9258 - val_acc: 0.6890
Epoch 7/30
1094/1094 [==============================] - 9s 9ms/step - loss: 0.2955 - acc: 0.9148 - val_loss: 0.9397 - val_acc: 0.6891
Epoch 8/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.2227 - acc: 0.9409 - val_loss: 0.9765 - val_acc: 0.6963
Epoch 9/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.1684 - acc: 0.9578 - val_loss: 1.0466 - val_acc: 0.6809
Epoch 10/30
1094/1094 [==============================] - 9s 8ms/step - loss: 0.1301 - acc: 0.9681 - val_loss: 1.0671 - val_acc: 0.6885
Epoch 11/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.1129 - acc: 0.9720 - val_loss: 1.1827 - val_acc: 0.6745
Epoch 12/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0904 - acc: 0.9781 - val_loss: 1.3506 - val_acc: 0.6476
Epoch 13/30
1094/1094 [==============================] - 9s 8ms/step - loss: 0.0827 - acc: 0.9792 - val_loss: 1.1821 - val_acc: 0.6833
Epoch 14/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0695 - acc: 0.9825 - val_loss: 1.3001 - val_acc: 0.6736
Epoch 15/30
1094/1094 [==============================] - 10s 9ms/step - loss: 0.0732 - acc: 0.9797 - val_loss: 1.2434 - val_acc: 0.6888
Epoch 16/30
1094/1094 [==============================] - 9s 8ms/step - loss: 0.0631 - acc: 0.9837 - val_loss: 1.3697 - val_acc: 0.6631
Epoch 17/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0650 - acc: 0.9820 - val_loss: 1.4061 - val_acc: 0.6619
Epoch 18/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0533 - acc: 0.9858 - val_loss: 1.3328 - val_acc: 0.6858
Epoch 19/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0556 - acc: 0.9837 - val_loss: 1.3194 - val_acc: 0.6857
Epoch 20/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0544 - acc: 0.9842 - val_loss: 1.3380 - val_acc: 0.6845
Epoch 21/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0442 - acc: 0.9885 - val_loss: 1.4235 - val_acc: 0.6781
Epoch 22/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0453 - acc: 0.9866 - val_loss: 1.4280 - val_acc: 0.6785
Epoch 23/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0472 - acc: 0.9862 - val_loss: 1.4123 - val_acc: 0.6768
Epoch 24/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0424 - acc: 0.9880 - val_loss: 1.4592 - val_acc: 0.6754
Epoch 25/30
1094/1094 [==============================] - 9s 8ms/step - loss: 0.0467 - acc: 0.9859 - val_loss: 1.4767 - val_acc: 0.6763
Epoch 26/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0390 - acc: 0.9883 - val_loss: 1.4459 - val_acc: 0.6842
Epoch 27/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0369 - acc: 0.9893 - val_loss: 1.4960 - val_acc: 0.6807
Epoch 28/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0426 - acc: 0.9867 - val_loss: 1.4734 - val_acc: 0.6857
Epoch 29/30
1094/1094 [==============================] - 10s 9ms/step - loss: 0.0331 - acc: 0.9901 - val_loss: 1.6271 - val_acc: 0.6669
Epoch 30/30
1094/1094 [==============================] - 8s 8ms/step - loss: 0.0417 - acc: 0.9870 - val_loss: 1.5915 - val_acc: 0.6756
import matplotlib.pyplot as plt
his_dict = history.history
loss = his_dict['loss']
val_loss = his_dict['val_loss']
epochs = range(1, len(loss)+1)
fig = plt.figure(figsize=(10, 5))
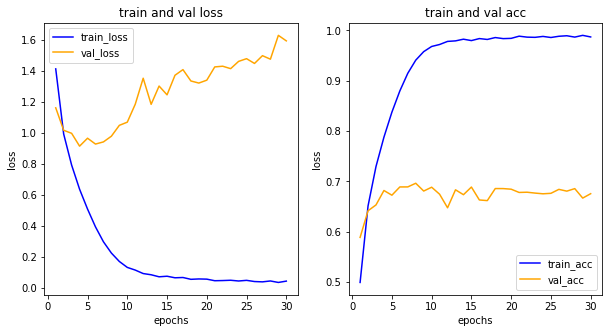
# 손실 그리기
ax1 = fig.add_subplot(1, 2, 1)
ax1.plot(epochs, loss, color='blue', label='train_loss')
ax1.plot(epochs, val_loss, color='orange', label='val_loss')
ax1.set_title('train and val loss')
ax1.set_xlabel('epochs')
ax1.set_ylabel('loss')
ax1.legend()
acc = his_dict['acc']
val_acc = his_dict['val_acc']
# 정확도 그리기
ax2 = fig.add_subplot(1, 2, 2)
ax2.plot(epochs, acc, color='blue', label='train_acc')
ax2.plot(epochs, val_acc, color='orange', label='val_acc')
ax2.set_title('train and val acc')
ax2.set_xlabel('epochs')
ax2.set_ylabel('loss')
ax2.legend()
<matplotlib.legend.Legend at 0x7f3c446aed30>
Reference
- 이 포스트는 SeSAC 인공지능 자연어처리, 컴퓨터비전 기술을 활용한 응용 SW 개발자 양성 과정 - 심선조 강사님의 강의를 정리한 내용입니다.

댓글남기기