Machine Learning (13) - 분류 / 신용카드 사기 검출

2022년 12월 01일 6 분 소요

분류

분류 실습 - 캐글 신용카드 사기 검출

언더 샘플링과 오버 샘플링의 이해

레이블이 불균형한 분포를 가진 데이터 세트를 학습시킬 때 이상 레이블을 가지는 데이터 건수가 정상 레이블을 가진 데이터 건수에 비해 너무 적기 때문에 문제가 발생할 수 있다.

언더 샘플링: 많은 데이터 세트를 적은 데이터 세트 수준으로 감소시키는 방식
오버 샘플링: 이상 데이터와 같이 적은 데이터 세트를 증식항 학습을 위한 충분한 데이터를 확보하는 방법

데이터 일차 가공 및 모델 학습/예측/평가

In [1]:

import pandas as pd
import numpy as np 
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")

In [2]:

card_df = pd.read_csv('creditcard.csv')
card_df.head(3)

Out [2]:

	Time	V1	V2	V3	V4	V5	V6	V7	V8	V9	...	V21	V22	V23	V24	V25	V26	V27	V28	Amount
0	0.0	-1.359807	-0.072781	2.536347	1.378155	-0.338321	0.462388	0.239599	0.098698	0.363787	...	-0.018307	0.277838	-0.110474	0.066928	0.128539	-0.189115	0.133558	-0.021053	149.62
1	0.0	1.191857	0.266151	0.166480	0.448154	0.060018	-0.082361	-0.078803	0.085102	-0.255425	...	-0.225775	-0.638672	0.101288	-0.339846	0.167170	0.125895	-0.008983	0.014724	2.69
2	1.0	-1.358354	-1.340163	1.773209	0.379780	-0.503198	1.800499	0.791461	0.247676	-1.514654	...	0.247998	0.771679	0.909412	-0.689281	-0.327642	-0.139097	-0.055353	-0.059752	378.66

3 rows × 31 columns

In [3]:

from sklearn.model_selection import train_test_split

# 인자로 입력받은 DataFrame을 복사 한 뒤 Time 컬럼만 삭제하고 복사된 DataFrame 반환
def get_preprocessed_df(df=None):
    df_copy = df.copy()
    df_copy.drop('Time', axis=1, inplace=True)
    return df_copy

In [4]:

# 사전 데이터 가공 후 학습과 테스트 데이터 세트를 반환하는 함수.
def get_train_test_dataset(df=None):
    # 인자로 입력된 DataFrame의 사전 데이터 가공이 완료된 복사 DataFrame 반환
    df_copy = get_preprocessed_df(df)
    # DataFrame의 맨 마지막 컬럼이 레이블, 나머지는 피처들
    X_features = df_copy.iloc[:, :-1]
    y_target = df_copy.iloc[:, -1]
    # train_test_split( )으로 학습과 테스트 데이터 분할. stratify=y_target으로 Stratified 기반 분할
    X_train, X_test, y_train, y_test = train_test_split(X_features, y_target,
                                                        test_size=0.3, random_state=0, stratify=y_target)
    # 학습과 테스트 데이터 세트 반환
    return X_train, X_test, y_train, y_test

X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)

In [5]:

# 레이블 불균형 확인
print('학습 데이터 레이블 값 비율')
print(y_train.value_counts()/y_train.shape[0] * 100)
print('테스트 데이터 레이블 값 비율')
print(y_test.value_counts()/y_test.shape[0] * 100)

Out [5]:

학습 데이터 레이블 값 비율
0    99.827451
1     0.172549
Name: Class, dtype: float64
테스트 데이터 레이블 값 비율
0    99.826785
1     0.173215
Name: Class, dtype: float64

In [6]:

# 평가점수 함수
from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score
from sklearn.metrics import roc_auc_score

def get_clf_eval(y_test, pred=None, pred_proba=None):
    confusion = confusion_matrix( y_test, pred)
    accuracy = accuracy_score(y_test , pred)
    precision = precision_score(y_test , pred)
    recall = recall_score(y_test , pred)
    f1 = f1_score(y_test,pred)
    # ROC-AUC 추가 
    roc_auc = roc_auc_score(y_test, pred_proba)
    print('오차 행렬')
    print(confusion)
    # ROC-AUC print 추가
    print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f},\
    F1: {3:.4f}, AUC:{4:.4f}'.format(accuracy, precision, recall, f1, roc_auc))

In [7]:

from sklearn.linear_model import LogisticRegression

lr_clf = LogisticRegression()
lr_clf.fit(X_train, y_train)
lr_pred = lr_clf.predict(X_test)
lr_pred_proba = lr_clf.predict_proba(X_test)[:, 1]

# 3장에서 사용한 get_clf_eval() 함수를 이용하여 평가 수행. 
get_clf_eval(y_test, lr_pred, lr_pred_proba)

Out [7]:

오차 행렬
[[85281    14]
 [   58    90]]
정확도: 0.9992, 정밀도: 0.8654, 재현율: 0.6081,    F1: 0.7143, AUC:0.9543

In [8]:

# 인자로 사이킷런의 Estimator객체와, 학습/테스트 데이터 세트를 입력 받아서 학습/예측/평가 수행하는 함수
def get_model_train_eval(model, ftr_train=None, ftr_test=None, tgt_train=None, tgt_test=None):
    model.fit(ftr_train, tgt_train)
    pred = model.predict(ftr_test)
    pred_proba = model.predict_proba(ftr_test)[:, 1]
    get_clf_eval(tgt_test, pred, pred_proba)

In [9]:

from lightgbm import LGBMClassifier

lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)

Out [9]:

오차 행렬
[[85290     5]
 [   36   112]]
정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568,    F1: 0.8453, AUC:0.9790

==로지스틱 회귀==
오차 행렬
[[85281 14]
[ 58 90]]
정확도: 0.9992, 정밀도: 0.8654, 재현율: 0.6081, F1: 0.7143, AUC:0.9543

데이터 분포도 변환 후 모델 학습/예측/평가

In [10]:

import seaborn as sns

plt.figure(figsize=(8, 4))
plt.xticks(range(0, 30000, 1000), rotation=60)
sns.histplot(card_df['Amount'], bins=100, kde=True)
plt.show()

Out [10]:

In [11]:

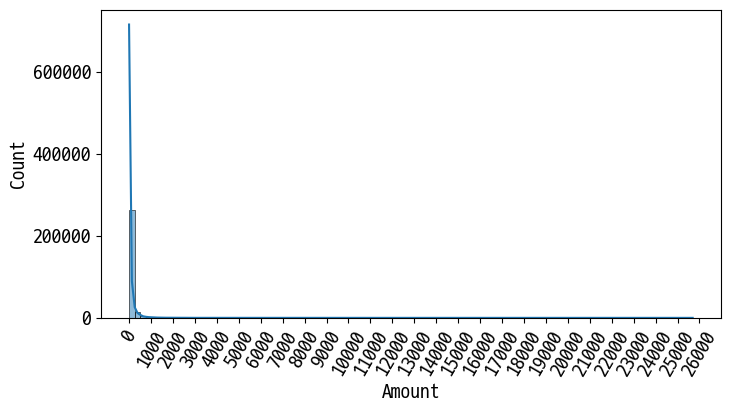
# 정규 분포 형태로 변환
from sklearn.preprocessing import StandardScaler

# 사이킷런의 StandardScaler를 이용하여 정규분포 형태로 Amount 피처값 변환하는 로직으로 수정. 
def get_preprocessed_df(df=None):
    df_copy = df.copy()
    scaler = StandardScaler()
    amount_n = scaler.fit_transform(df_copy['Amount'].values.reshape(-1, 1))
    # 변환된 Amount를 Amount_Scaled로 피처명 변경후 DataFrame맨 앞 컬럼으로 입력
    df_copy.insert(0, 'Amount_Scaled', amount_n)
    # 기존 Time, Amount 피처 삭제
    df_copy.drop(['Time','Amount'], axis=1, inplace=True)
    return df_copy

In [12]:

# Amount를 정규분포 형태로 변환 후 로지스틱 회귀 및 LightGBM 수행. 
X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)

In [13]:

X_train.head(1)

Out [13]:

	Amount_Scaled	V1	V2	V3	V4	V5	V6	V7	V8	V9	...	V19	V20	V21	V22	V23	V24	V25	V26	V27	V28
211605	-0.350471	-8.367621	7.402969	-5.114191	-2.966792	-0.985904	-1.660018	0.397816	1.00825	5.290976	...	-0.750795	3.589299	-0.557927	0.349087	0.301734	0.66233	1.145939	-0.012273	1.513736	0.669504

1 rows × 29 columns

In [14]:

print('### 로지스틱 회귀 예측 성능 ###')
lr_clf = LogisticRegression()
get_model_train_eval(lr_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)

print('### LightGBM 예측 성능 ###')
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)

Out [14]:

### 로지스틱 회귀 예측 성능 ###
오차 행렬
[[85281    14]
 [   58    90]]
정확도: 0.9992, 정밀도: 0.8654, 재현율: 0.6081,    F1: 0.7143, AUC:0.9702
### LightGBM 예측 성능 ###
오차 행렬
[[85290     5]
 [   37   111]]
정확도: 0.9995, 정밀도: 0.9569, 재현율: 0.7500,    F1: 0.8409, AUC:0.9779

StandardScaler 적용 전

==로지스틱 회귀==
오차 행렬
[[85281 14]
[ 58 90]]
정확도: 0.9992, 정밀도: 0.8654, 재현율: 0.6081, F1: 0.7143, AUC:0.9543

==LightGBM==
오차 행렬
[[85290 5]
[ 36 112]]
정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568, F1: 0.8453, AUC:0.9790

In [15]:

# 데이터 로그화(정규 분포화)
def get_preprocessed_df(df=None):
    df_copy = df.copy()
    # 넘파이의 log1p( )를 이용하여 Amount를 로그 변환 
    amount_n = np.log1p(df_copy['Amount'])
    df_copy.insert(0, 'Amount_Scaled', amount_n)
    df_copy.drop(['Time','Amount'], axis=1, inplace=True)
    return df_copy

In [16]:

X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)

print('### 로지스틱 회귀 예측 성능 ###')
get_model_train_eval(lr_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)

print('### LightGBM 예측 성능 ###')
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)

Out [16]:

### 로지스틱 회귀 예측 성능 ###
오차 행렬
[[85283    12]
 [   59    89]]
정확도: 0.9992, 정밀도: 0.8812, 재현율: 0.6014,    F1: 0.7149, AUC:0.9727
### LightGBM 예측 성능 ###
오차 행렬
[[85290     5]
 [   35   113]]
정확도: 0.9995, 정밀도: 0.9576, 재현율: 0.7635,    F1: 0.8496, AUC:0.9796

데이터 로그화 전

==로지스틱 회귀==
오차 행렬
[[85281 14]
[ 58 90]]
정확도: 0.9992, 정밀도: 0.8654, 재현율: 0.6081, F1: 0.7143, AUC:0.9543

==LightGBM==
오차 행렬
[[85290 5]
[ 36 112]]
정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568, F1: 0.8453, AUC:0.9790

이상치 데이터 제거 후 모델 학습/예측/평가

In [17]:

# 상관관계 확인
import seaborn as sns

plt.figure(figsize=(9, 9))
corr = card_df.corr()
sns.heatmap(corr, cmap='RdBu')

Out [17]:

<AxesSubplot:>

In [18]:

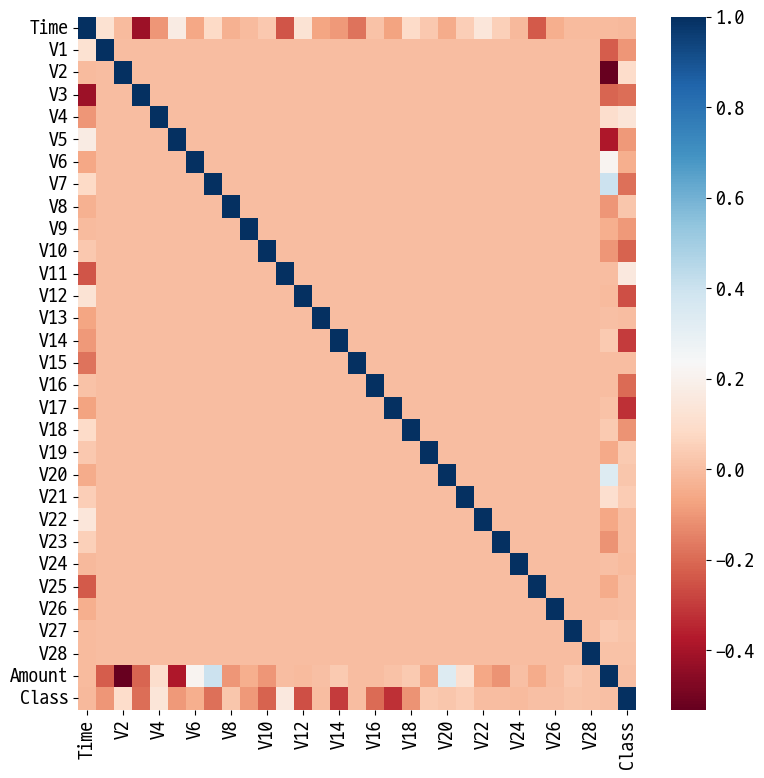
import numpy as np

def get_outlier(df=None, column=None, weight=1.5):
    # fraud에 해당하는 column 데이터만 추출, 1/4 분위와 3/4 분위 지점을 np.percentile로 구함. 
    fraud = df[df['Class']==1][column]
    quantile_25 = np.percentile(fraud.values, 25)
    quantile_75 = np.percentile(fraud.values, 75)
    # IQR을 구하고, IQR에 1.5를 곱하여 최대값과 최소값 지점 구함. 
    iqr = quantile_75 - quantile_25
    iqr_weight = iqr * weight
    lowest_val = quantile_25 - iqr_weight
    highest_val = quantile_75 + iqr_weight
    # 최대값 보다 크거나, 최소값 보다 작은 값을 아웃라이어로 설정하고 DataFrame index 반환. 
    outlier_index = fraud[(fraud < lowest_val) | (fraud > highest_val)].index
    return outlier_index

In [19]:

outlier_index = get_outlier(df=card_df, column='V17', weight=1.5)
print('이상치 데이터 인덱스:', outlier_index)

Out [19]:

이상치 데이터 인덱스: Int64Index([], dtype='int64')

In [20]:

outlier_index = get_outlier(df=card_df, column='V14', weight=1.5)
print('이상치 데이터 인덱스:', outlier_index)

Out [20]:

이상치 데이터 인덱스: Int64Index([8296, 8615, 9035, 9252], dtype='int64')

In [21]:

outlier_index = get_outlier(df=card_df, column='V12', weight=1.5)
print('이상치 데이터 인덱스:', outlier_index)

Out [21]:

이상치 데이터 인덱스: Int64Index([8296, 8615, 150601, 150644, 150647, 150654], dtype='int64')

In [22]:

# get_processed_df( )를 로그 변환 후 V14 피처의 이상치 데이터를 삭제하는 로직으로 변경. 
def get_preprocessed_df(df=None):
    df_copy = df.copy()
    amount_n = np.log1p(df_copy['Amount'])
    df_copy.insert(0, 'Amount_Scaled', amount_n)
    df_copy.drop(['Time','Amount'], axis=1, inplace=True)
    # 이상치 데이터 삭제하는 로직 추가
    outlier_index = get_outlier(df=df_copy, column='V14', weight=1.5)
    df_copy.drop(outlier_index, axis=0, inplace=True)
    return df_copy

X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
print('### 로지스틱 회귀 예측 성능 ###')
get_model_train_eval(lr_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)
print('### LightGBM 예측 성능 ###')
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)

Out [22]:

### 로지스틱 회귀 예측 성능 ###
오차 행렬
[[85281    14]
 [   48    98]]
정확도: 0.9993, 정밀도: 0.8750, 재현율: 0.6712,    F1: 0.7597, AUC:0.9743
### LightGBM 예측 성능 ###
오차 행렬
[[85290     5]
 [   25   121]]
정확도: 0.9996, 정밀도: 0.9603, 재현율: 0.8288,    F1: 0.8897, AUC:0.9780

이상치 제거전

==로지스틱 회귀 예측 성능==
오차 행렬
[[85283 12]
[ 59 89]]
정확도: 0.9992, 정밀도: 0.8812, 재현율: 0.6014, F1: 0.7149, AUC:0.9727
==LightGBM 예측 성능==
오차 행렬
[[85290 5]
[ 35 113]]
정확도: 0.9995, 정밀도: 0.9576, 재현율: 0.7635, F1: 0.8496, AUC:0.9796

SMOTE 오버 샘플링 적용 후 모델 학습/예측/평가

In [23]:

from imblearn.over_sampling import SMOTE

smote = SMOTE(random_state=0)
X_train_over, y_train_over = smote.fit_resample(X_train, y_train)
print('SMOTE 적용 전 학습용 피처/레이블 데이터 세트: ', X_train.shape, y_train.shape)
print('SMOTE 적용 후 학습용 피처/레이블 데이터 세트: ', X_train_over.shape, y_train_over.shape)
print('SMOTE 적용 후 레이블 값 분포: \n', pd.Series(y_train_over).value_counts())

Out [23]:

SMOTE 적용 전 학습용 피처/레이블 데이터 세트:  (199362, 29) (199362,)
SMOTE 적용 후 학습용 피처/레이블 데이터 세트:  (398040, 29) (398040,)
SMOTE 적용 후 레이블 값 분포: 
 0    199020
1    199020
Name: Class, dtype: int64

In [24]:

lr_clf = LogisticRegression()

# ftr_train과 tgt_train 인자값이 SMOTE 증식된 X_train_over와 y_train_over로 변경됨에 유의
get_model_train_eval(lr_clf, ftr_train=X_train_over, ftr_test=X_test, tgt_train=y_train_over, tgt_test=y_test)

Out [24]:

오차 행렬
[[82937  2358]
 [   11   135]]
정확도: 0.9723, 정밀도: 0.0542, 재현율: 0.9247,    F1: 0.1023, AUC:0.9737

오버 샘플링 전

==로지스틱 회귀==
오차 행렬
[[85281 14]
[ 58 90]]
정확도: 0.9992, 정밀도: 0.8654, 재현율: 0.6081, F1: 0.7143, AUC:0.9543

In [25]:

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.metrics import precision_recall_curve

In [26]:

def precision_recall_curve_plot(y_test , pred_proba_c1):
    # threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출. 
    precisions, recalls, thresholds = precision_recall_curve( y_test, pred_proba_c1)
    
    # X축을 threshold값으로, Y축은 정밀도, 재현율 값으로 각각 Plot 수행. 정밀도는 점선으로 표시
    plt.figure(figsize=(8,6))
    threshold_boundary = thresholds.shape[0]
    plt.plot(thresholds, precisions[0:threshold_boundary], linestyle='--', label='precision')
    plt.plot(thresholds, recalls[0:threshold_boundary],label='recall')
    
    # threshold 값 X 축의 Scale을 0.1 단위로 변경
    start, end = plt.xlim()
    plt.xticks(np.round(np.arange(start, end, 0.1),2))
    
    # x축, y축 label과 legend, 그리고 grid 설정
    plt.xlabel('Threshold value'); plt.ylabel('Precision and Recall value')
    plt.legend(); plt.grid()
    plt.show()

In [27]:

precision_recall_curve_plot( y_test, lr_clf.predict_proba(X_test)[:, 1] )

Out [27]:

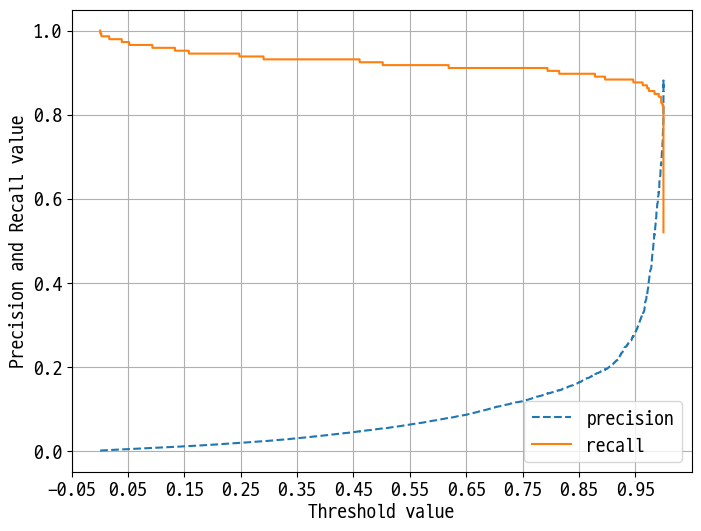
한쪽으로 쏠려서 나타남!

In [28]:

lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
get_model_train_eval(lgbm_clf, ftr_train=X_train_over, ftr_test=X_test,
                  tgt_train=y_train_over, tgt_test=y_test)

Out [28]:

오차 행렬
[[85283    12]
 [   22   124]]
정확도: 0.9996, 정밀도: 0.9118, 재현율: 0.8493,    F1: 0.8794, AUC:0.9814

오버 샘플링 전

==LightGBM==
오차 행렬
[[85290 5]
[ 36 112]]
정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568, F1: 0.8453, AUC:0.9790

로지스틱 회귀는 회귀를 기반으로 하고 LightGBM은 트리 기반으로 하는 둘의 로직 차이로 오버 샘플링에 이상 유무가 나옴

Reference

이 포스트는 SeSAC 인공지능 자연어처리, 컴퓨터비전 기술을 활용한 응용 SW 개발자 양성 과정 - 심선조 강사님의 강의를 정리한 내용입니다.

Twitter Facebook LinkedIn

Kwak Jisub

Machine Learning (13) - 분류 / 신용카드 사기 검출

분류

분류 실습 - 캐글 신용카드 사기 검출

언더 샘플링과 오버 샘플링의 이해

데이터 일차 가공 및 모델 학습/예측/평가

데이터 분포도 변환 후 모델 학습/예측/평가

이상치 데이터 제거 후 모델 학습/예측/평가

SMOTE 오버 샘플링 적용 후 모델 학습/예측/평가

Reference

공유하기

댓글남기기

참고

python max 함수의 매개변수

python round 함수의 문제

python set 자료형과 메소드

MySQL GROUP BY와 MAX