Kwak Jisub

정리를 미루지 말자!

새싹 AI 프로그래머
화이팅!

2 분 소요

회귀

  • 독립변수 : 회귀에서 입력값은 독립적이어야 한다.
    입력변수들 사이에 연관관계가 있다면 다중공선성 문제가 생긴다. -> PCA

  • 종속변수 : 독립변수의 변화에 영향을 받는 결과
    종속변수에 영향력을 가지는 독립변수를 선택해야 한다.

머신러닝 회귀 예측의 핵심은 주어진 피처와 결정 값 데이터 기산에서 학습을 통해 최적의 회귀 계수(Regression coefficients)를 찾아내는 것이다.

여러 가지 회귀 중에서 선형 회귀가 가장 많이 사용된다. 실제값과 예측값의 차이를 최소화 하는 직선형 회귀선을 최적화하는 방식이다. 선형 회귀 모델은 규제(Regularization) 방법에 따라 다시 별도의 유형으로 나뉜다. 규제는 일반적인 선형 회귀의 과적합 문제를 해결하기 위해 회귀 계수에 페널티 값을 적용하는 것을 말한다.

  • 대표적 선형 회귀 모델
    1. 일반 선형 회귀: 예측값과 실제값의 RSS(Residual Sum of Squares)를 최소화할 수 있도록 회귀 계수를 최적화하며, 규제를 적용하지 않는 모델

  1. 릿지(Ridge): 선형 회귀에 L2 규제를 추가한 회귀 모델. 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소(0에 가까운 값으로 줄임)시키기 위해 회귀 계수값을 더 작게 만드는 규제 모델

  2. 라쏘(Lasso): 선형 회귀에 L1 규제를 적용. L2 규제가 회귀 계수 값의 크기를 줄이지만 L1 규제는 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어 회귀 예측 시 피처가 선택되지 않게 함(피처 선택 기능)

  3. 엘라스틱넷(ElasticNet): L2, L1 규제를 함께 결합한 모델. 주로 피처가 많은 데이터 세트에서 적용. L1 규제로 피처의 개수를 줄임과 동시에 L2 규제로 계수값의 크기를 조정

  4. 로지스틱 회귀(Logistic Regression): 회귀라는 이름이 붙어 있지만 분류에 사용되는 선형 모델. 매우 강력한 분류 알고리즘. 일반적으로 이진 분류뿐만 아니라 희소 영역의 분류에서 뛰어난 예측 성능을 보임

RSS(Residual Sum of Square): 오류값의 제곱을 구해서 더하는 방식 비용함수(손실함수;loss function): 회귀에서 RSS는 비용(Cost)이며 w변수(회귀 계수)로 구성되는 RSS

\[RSS(w_0,w_1)=\frac{1}{N}\sum^N_{i=0}(y_i-(w_0+w_1*x_i))^2\]

경사 하강법(Gradient Descent)

점진적으로 반복적인 계산을 통해 w파라미터 값을 업데이트하면서 오류값이 최소가 되는 w파라미터를 구하는 방식

In [1]: 
import numpy as np
import matplotlib.pyplot as plt

np.random

  • seed : seed를 통한 난수 생성
  • randint : 균일 분포의 정수 난수 1개 생성
  • rand : 0~1사이의 균일 분포에서 난수 matrix array 생성
  • randn : 가우시안 정규 분포에서 난수 matrix array 생성
In [2]: 
np.random.seed(0)

# y = 4X + 6을 근사(w1=4, w0=6). 임의의 값은 노이즈를 위해 만듦
X = 2 * np.random.rand(100, 1)
y = 6 + 4 * X + np.random.randn(100, 1) # 노이즈를 더해줌

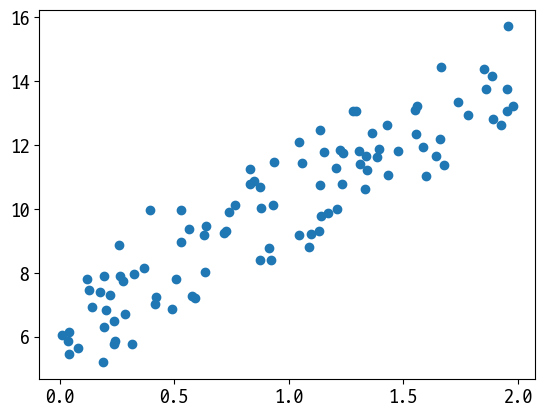
plt.scatter(X, y)
Out [2]: 
<matplotlib.collections.PathCollection at 0x2620b3f2400>

img

In [3]: 
# 편미분 하는 함수
def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
    N = len(y)
    
    # w1, w0와 동일한 모양의 안을 0으로 채워 초기화
    w1_update = np.zeros_like(w1)
    w0_update = np.zeros_like(w0)
    y_pred = np.dot(X, w1.T) + w0 # dot: 행렬곱 # T: transpose로 행렬곱이 가능한 형태로 변환
    diff = y - y_pred
    
    # w0_update를 dot 행렬 연산으로 구하기 위해 모두 1값을 가진 행렬 생성
    w0_factors = np.ones((N, 1))
    
    # w1과 w0을 업데이트할 w1_update와 w0_update 계산
    w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff))
    w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff))
    
    return w1_update, w0_update
In [4]: 
# 경사 하강 방식으로 반복적으로 수행하여 w1과 w0를 업데이트 적용하는 함수
def gradient_descent_steps(X, y, iters=10000):
    # w0, w1을 모두 0으로 초기화
    w0 = np.zeros((1, 1)) # 들어오는 변수가 1개이므로 1행1열
    w1 = np.zeros((1, 1))
    
    for ind in range(iters):
        w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
        w1 = w1 - w1_update # 편미분한 값(기울기)이 +라면 w를 감소시겨야 하므로 - 해줌
        w0 = w0 - w0_update
        
    return w1, w0
In [5]: 
# 오차 계산 함수(비용함수)
def get_cost(y, y_pred):
    N = len(y)
    cost = np.sum(np.square(y - y_pred)) / N
    return cost
In [6]: 
w1, w0 = gradient_descent_steps(X, y, iters=1000)
In [7]: 
print(f'w1: {w1[0, 0]:.3f} w0: {w0[0, 0]:.3f}')
Out [7]: 
w1: 4.022 w0: 6.162
In [8]: 
y_pred = w1[0, 0] * X + w0
print(f'Gradient Descent Total Cost: {get_cost(y, y_pred):.4f}')
Out [8]: 
Gradient Descent Total Cost: 0.9935
In [9]: 
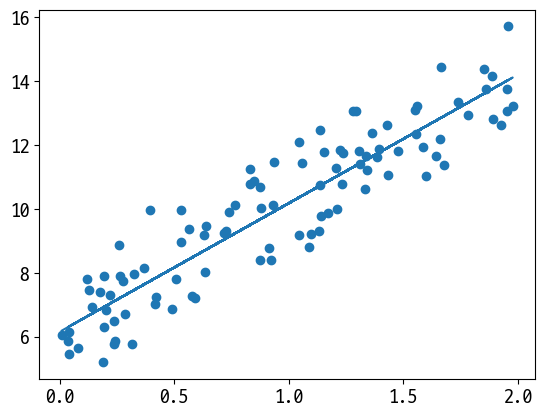
plt.scatter(X, y)
plt.plot(X, y_pred)
Out [9]: 
[<matplotlib.lines.Line2D at 0x2620b454370>]

img

Reference

  • 이 포스트는 SeSAC 인공지능 자연어처리, 컴퓨터비전 기술을 활용한 응용 SW 개발자 양성 과정 - 심선조 강사님의 강의를 정리한 내용입니다.

댓글남기기

참고