Machine Learning (15) - 회귀 / 선형 회귀
회귀
사이킷런 LinearRegression을 이용한 보스턴 주택 가격 예측
LinearRegression 클래스
입력 파라미터
- fit_inptercept[default=True]: 절편 값 계산 여부
- normalize[default=False]: 회귀 수행 전 입력 데이터 세트 정규화
속성
- coef_: fit() 수행시 가중치(회귀 계수) 저장
-
intercept_: 바이어스(졀편)
- 다중 공선성(multi-collinearity)
Ordinary Least Squares 기반의 회귀 계수 계산은 입력 피처의 독립성에 많은 영향을 받는다. 피처 간의 상관관계가 매우 높은 경우 분산이 매우 커져서 오류에 매우 민감해진다.
회귀 평가 지표
회귀 평가를 위한 지표는 실제 값과 회귀 예측값의 차이 값을 기반으로 한 지표이다.
- MAE(Mean Absolute Error): 절대값으로 변환해 평균
- MSE(Mean Squared Error): 제곱해 평균
- RMSE(Root Mean Squared Error): 제곱해 평균(MSE) 구하고 루트
- MSLE(Mean Squared Log Error): MSE에 log적용
- RMSLE(Root Mean Squared Log Error): RMSE에 log적용
- \(R^2\): 분산 기반으로 평가. 실제값 분산 대비 예측값 분산 비율을 지표로 1에 가까울수록 예측 정확도가 높음
사이킷런의 Scoring 함수가 score값이 클수록 좋은 평가 결과로 자동 평가하기 때문에 위의 지표에 -1을 곱해 보정을 한다. scoring파라미터 값으로 주어지는 neg_*는 해당 API의 결과값에 -1을 곱한 값이므로 주의가 필요하다.
LinearRegression을 이용해 보스턴 주택 가격 회귀 구현
In [1]:
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.datasets import load_boston
import warnings
warnings.filterwarnings('ignore')
In [2]:
boston = load_boston()
In [3]:
df = pd.DataFrame(boston.data, columns=boston.feature_names)
In [4]:
df['PRICE'] = boston.target
In [5]:
df.sample(3)
Out [5]:
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | PRICE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 311 | 0.79041 | 0.0 | 9.90 | 0.0 | 0.544 | 6.122 | 52.8 | 2.6403 | 4.0 | 304.0 | 18.4 | 396.90 | 5.98 | 22.1 |
| 424 | 8.79212 | 0.0 | 18.10 | 0.0 | 0.584 | 5.565 | 70.6 | 2.0635 | 24.0 | 666.0 | 20.2 | 3.65 | 17.16 | 11.7 |
| 53 | 0.04981 | 21.0 | 5.64 | 0.0 | 0.439 | 5.998 | 21.4 | 6.8147 | 4.0 | 243.0 | 16.8 | 396.90 | 8.43 | 23.4 |
In [6]:
df.info()
Out [6]:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 506 entries, 0 to 505
Data columns (total 14 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 CRIM 506 non-null float64
1 ZN 506 non-null float64
2 INDUS 506 non-null float64
3 CHAS 506 non-null float64
4 NOX 506 non-null float64
5 RM 506 non-null float64
6 AGE 506 non-null float64
7 DIS 506 non-null float64
8 RAD 506 non-null float64
9 TAX 506 non-null float64
10 PTRATIO 506 non-null float64
11 B 506 non-null float64
12 LSTAT 506 non-null float64
13 PRICE 506 non-null float64
dtypes: float64(14)
memory usage: 55.5 KB
In [7]:
df.columns
Out [7]:
Index(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
'PTRATIO', 'B', 'LSTAT', 'PRICE'],
dtype='object')
In [8]:
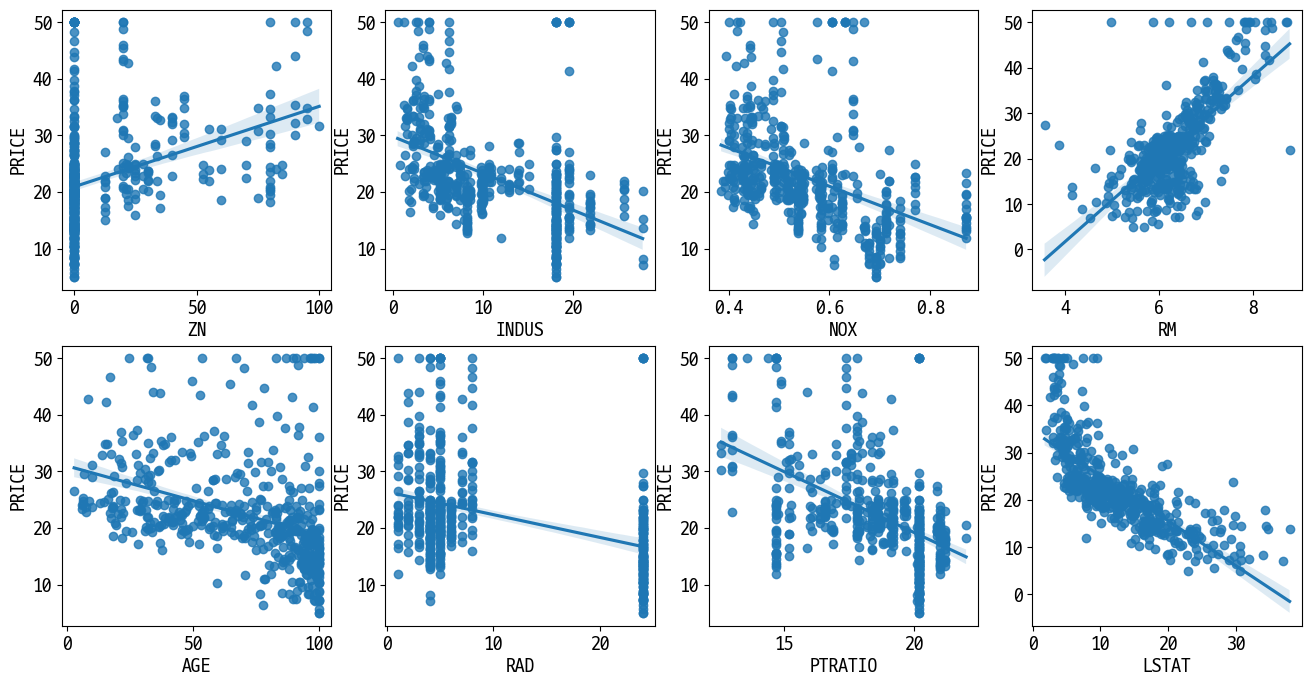
# 각 컬럼이 회귀 결과에 미치는 영향이 어느 정도인지 시각화
lm_features = ['ZN', 'INDUS', 'NOX', 'RM', 'AGE', 'RAD', 'PTRATIO', 'LSTAT',]
fig, axs = plt.subplots(figsize=(16, 8), ncols=4, nrows=2)
for i , feature in enumerate(lm_features):
row = int(i / 4)
col = i % 4
# seaborn의 regplot을 이용해 산점도와 선형 회귀 직선을 함께 표현
sns.regplot(x=feature, y='PRICE', data=df, ax=axs[row][col])
Out [8]:
- 회귀 모델 만들기
In [9]:
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
In [10]:
y = df['PRICE']
X = df.drop(columns='PRICE')
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=156)
In [11]:
# 선형 회귀 OLS로 학습/예측/평가 수행
lr = LinearRegression()
lr.fit(X_train, y_train)
pred = lr.predict(X_test)
mse = mean_squared_error(y_test, pred)
rmse = np.sqrt(mse) # = mean_squared_error(y_test, pred, squared=False)
print(f'MSE: {mse:.3f}, RMSE: {rmse:.3f}, R2: {r2_score(y_test, pred):.3f}')
Out [11]:
MSE: 17.297, RMSE: 4.159, R2: 0.757
In [12]:
print(f'절편값: {lr.intercept_}')
print(f'회귀 계수값: {np.round(lr.coef_, 1)}')
Out [12]:
절편값: 40.99559517216444
회귀 계수값: [ -0.1 0.1 0. 3. -19.8 3.4 0. -1.7 0.4 -0. -0.9 0.
-0.6]
In [13]:
# 회귀 계수를 큰 값 순으로 정렬(Serise로 생성)
pd.Series(np.round(lr.coef_, 1), index=X.columns).sort_values(ascending=False)
Out [13]:
RM 3.4
CHAS 3.0
RAD 0.4
ZN 0.1
INDUS 0.0
AGE 0.0
TAX -0.0
B 0.0
CRIM -0.1
LSTAT -0.6
PTRATIO -0.9
DIS -1.7
NOX -19.8
dtype: float64
회귀 계수값이 크면 과적합 문제가 발생할 수 있다! -> 규제
In [14]:
# 교차 검증 확인
from sklearn.model_selection import cross_val_score
In [15]:
neg_mse_scores = cross_val_score(lr, X, y, scoring='neg_mean_squared_error', cv=5)
rmse_scores = np.sqrt(-1*neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
print(f'5 folds 개별 Negative MSE scores: {np.round(neg_mse_scores, 2)}')
print(f'5 folds 개별 RMSE scores: {np.round(rmse_scores, 2)}')
print(f'5 folds 평균 RMSE: {np.round(avg_rmse, 3)}')
Out [15]:
5 folds 개별 Negative MSE scores: [-12.46 -26.05 -33.07 -80.76 -33.31]
5 folds 개별 RMSE scores: [3.53 5.1 5.75 8.99 5.77]
5 folds 평균 RMSE: 5.829
규제 선형 모델 - 릿지, 라쏘, 엘라스틱넷
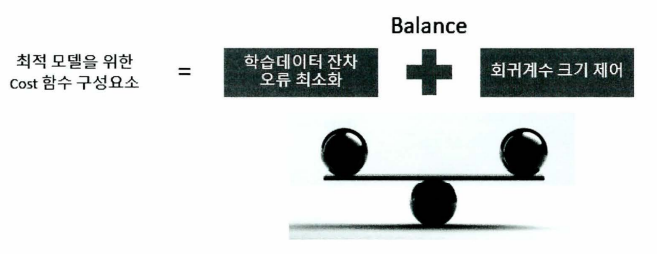
alpha 값을 크게 하면 비용 함수는 회귀 계수의 W값을 작게 해 과적합을 개선한다.
alpha 값을 작게 하면 회귀 계수 W의 값이 커져도 어느 정도 상쇄가 가능하므로 학습 데이터 적합을 더 개선한다.
- 규제(Regularization): 비용 함수에 alpha 값으로 페널티를 부여해 회귀 계수 값의 크기를 감소시켜 과적합을 개선하는 방식
- L2 규제: W의 제곱에 대해 페널티 부여. 릿지(Ridge) 회귀
- L1 규제: W의 절댓값에 대해 페널티 부여. 라쏘(Lasso) 회귀. L1 규제를 적용하면 영향력이 크지 않은 회귀 계수 값을 0으로 변환.
릿지 회귀
In [16]:
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
In [17]:
# alpha=10으로 설정해 릿지 회귀 수행
ridge = Ridge(alpha=10)
neg_mse_scores = cross_val_score(ridge, X, y, scoring='neg_mean_squared_error', cv=5)
rmse_scores = np.sqrt(-1*neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
print(f'5 folds 개별 Negative MSE scores: {np.round(neg_mse_scores, 2)}')
print(f'5 folds 개별 RMSE scores: {np.round(rmse_scores, 2)}')
print(f'5 folds 평균 RMSE: {np.round(avg_rmse, 3)}')
Out [17]:
5 folds 개별 Negative MSE scores: [-11.42 -24.29 -28.14 -74.6 -28.52]
5 folds 개별 RMSE scores: [3.38 4.93 5.31 8.64 5.34]
5 folds 평균 RMSE: 5.518
In [18]:
# 릿지에 사용될 alpha 파라미터 정의
alphas = [0, 0.1, 1, 10, 100]
# alpha list 값을 반복하면서 alpha에 따른 평균 rmse를 구함
for alpha in alphas:
ridge = Ridge(alpha=alpha)
neg_mse_scores = cross_val_score(ridge, X, y, scoring='neg_mean_squared_error', cv=5)
avg_rmse = np.mean(np.sqrt(-1*neg_mse_scores))
print(f'alpha {alpha}, 5 folds 평균 RMSE: {np.round(avg_rmse, 3)}')
Out [18]:
alpha 0, 5 folds 평균 RMSE: 5.829
alpha 0.1, 5 folds 평균 RMSE: 5.788
alpha 1, 5 folds 평균 RMSE: 5.653
alpha 10, 5 folds 평균 RMSE: 5.518
alpha 100, 5 folds 평균 RMSE: 5.33
In [19]:
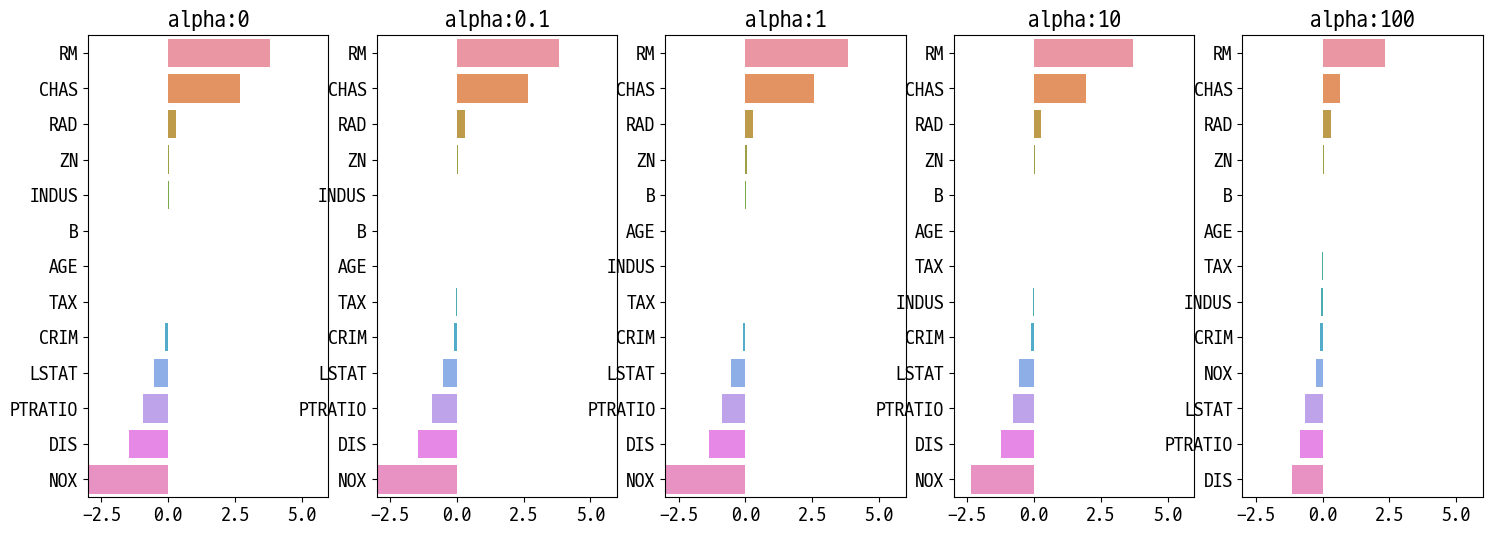
# alpha 값의 변화에 따른 피처의 회귀 계수값을 시각화
fig, axs = plt.subplots(figsize=(18, 6), nrows=1, ncols=5)
# alpha에 따른 회귀 계수값을 저장할 장소
coeff_df = pd.DataFrame()
for pos, alpha in enumerate(alphas):
ridge = Ridge(alpha=alpha)
ridge.fit(X, y)
# alpha에 따른 피처별 회귀 계수를 Series로 변환, DF에 추가
coeff = pd.Series(ridge.coef_, index=X.columns)
colname = 'alpha:' + str(alpha)
coeff_df[colname] = coeff
# barplot
coeff = coeff.sort_values(ascending=False)
axs[pos].set_title(colname)
axs[pos].set_xlim(-3, 6)
sns.barplot(x=coeff.values, y=coeff.index, ax=axs[pos])
plt.show()
Out [19]:
In [20]:
sort_column = 'alpha:' + str(alphas[0])
coeff_df.sort_values(by=sort_column, ascending=False)
Out [20]:
| alpha:0 | alpha:0.1 | alpha:1 | alpha:10 | alpha:100 | |
|---|---|---|---|---|---|
| RM | 3.809865 | 3.818233 | 3.854000 | 3.702272 | 2.334536 |
| CHAS | 2.686734 | 2.670019 | 2.552393 | 1.952021 | 0.638335 |
| RAD | 0.306049 | 0.303515 | 0.290142 | 0.279596 | 0.315358 |
| ZN | 0.046420 | 0.046572 | 0.047443 | 0.049579 | 0.054496 |
| INDUS | 0.020559 | 0.015999 | -0.008805 | -0.042962 | -0.052826 |
| B | 0.009312 | 0.009368 | 0.009673 | 0.010037 | 0.009393 |
| AGE | 0.000692 | -0.000269 | -0.005415 | -0.010707 | 0.001212 |
| TAX | -0.012335 | -0.012421 | -0.012912 | -0.013993 | -0.015856 |
| CRIM | -0.108011 | -0.107474 | -0.104595 | -0.101435 | -0.102202 |
| LSTAT | -0.524758 | -0.525966 | -0.533343 | -0.559366 | -0.660764 |
| PTRATIO | -0.952747 | -0.940759 | -0.876074 | -0.797945 | -0.829218 |
| DIS | -1.475567 | -1.459626 | -1.372654 | -1.248808 | -1.153390 |
| NOX | -17.766611 | -16.684645 | -10.777015 | -2.371619 | -0.262847 |
릿지(L2 규제)는 줄여는 주지만 0으로 만들지는 않는다!
라쏘 회귀
In [21]:
from sklearn.linear_model import Lasso, ElasticNet
In [22]:
# alpha값에 따른 회귀 모델의 폴드 평균 RMSE를 출력하고 회귀 계수값들을 DataFrame으로 반환
def get_linear_reg_eval(model_name, params=None, X_data_n=None, y_target_n=None,
verbose=True, return_coeff=True):
coeff_df = pd.DataFrame()
if verbose : print('####### ', model_name , '#######')
for param in params:
if model_name =='Ridge': model = Ridge(alpha=param)
elif model_name =='Lasso': model = Lasso(alpha=param)
elif model_name =='ElasticNet': model = ElasticNet(alpha=param, l1_ratio=0.7) # l1_ratio: L1과 L2의 비율
# 교차검증, 점수
neg_mse_scores = cross_val_score(model, X_data_n,
y_target_n, scoring="neg_mean_squared_error", cv = 5)
avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores))
print('alpha {0}일 때 5 폴드 세트의 평균 RMSE: {1:.3f} '.format(param, avg_rmse))
# cross_val_score는 evaluation metric만 반환하므로 모델을 다시 학습하여 회귀 계수 추출
model.fit(X_data_n , y_target_n)
if return_coeff:
# alpha에 따른 피처별 회귀 계수를 Series로 변환하고 이를 DataFrame의 컬럼으로 추가.
coeff = pd.Series(data=model.coef_ , index=X_data_n.columns )
colname='alpha:' + str(param)
coeff_df[colname] = coeff
return coeff_df
# end of get_linear_regre_eval
In [23]:
lasso_alphas = [0.07, 0.1, 0.5, 1, 3]
coeff_lasso_df = get_linear_reg_eval('Lasso', lasso_alphas, X, y)
Out [23]:
####### Lasso #######
alpha 0.07일 때 5 폴드 세트의 평균 RMSE: 5.612
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.615
alpha 0.5일 때 5 폴드 세트의 평균 RMSE: 5.669
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.776
alpha 3일 때 5 폴드 세트의 평균 RMSE: 6.189
In [24]:
sort_column = 'alpha:' + str(lasso_alphas[0])
coeff_lasso_df.sort_values(by=sort_column, ascending=False)
Out [24]:
| alpha:0.07 | alpha:0.1 | alpha:0.5 | alpha:1 | alpha:3 | |
|---|---|---|---|---|---|
| RM | 3.789725 | 3.703202 | 2.498212 | 0.949811 | 0.000000 |
| CHAS | 1.434343 | 0.955190 | 0.000000 | 0.000000 | 0.000000 |
| RAD | 0.270936 | 0.274707 | 0.277451 | 0.264206 | 0.061864 |
| ZN | 0.049059 | 0.049211 | 0.049544 | 0.049165 | 0.037231 |
| B | 0.010248 | 0.010249 | 0.009469 | 0.008247 | 0.006510 |
| NOX | -0.000000 | -0.000000 | -0.000000 | -0.000000 | 0.000000 |
| AGE | -0.011706 | -0.010037 | 0.003604 | 0.020910 | 0.042495 |
| TAX | -0.014290 | -0.014570 | -0.015442 | -0.015212 | -0.008602 |
| INDUS | -0.042120 | -0.036619 | -0.005253 | -0.000000 | -0.000000 |
| CRIM | -0.098193 | -0.097894 | -0.083289 | -0.063437 | -0.000000 |
| LSTAT | -0.560431 | -0.568769 | -0.656290 | -0.761115 | -0.807679 |
| PTRATIO | -0.765107 | -0.770654 | -0.758752 | -0.722966 | -0.265072 |
| DIS | -1.176583 | -1.160538 | -0.936605 | -0.668790 | -0.000000 |
alpha를 높일수록 회귀 계수가 0이 되는 피처가 늘어난다! -> 피처 선택의 효과
엘라스틱넷 회귀
In [25]:
elastic_alphas = [0.07, 0.1, 0.5, 1, 3]
coeff_elastic_df = get_linear_reg_eval('ElasticNet', elastic_alphas, X, y)
Out [25]:
####### ElasticNet #######
alpha 0.07일 때 5 폴드 세트의 평균 RMSE: 5.542
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.526
alpha 0.5일 때 5 폴드 세트의 평균 RMSE: 5.467
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.597
alpha 3일 때 5 폴드 세트의 평균 RMSE: 6.068
In [26]:
sort_column = 'alpha:' + str(elastic_alphas[0])
coeff_elastic_df.sort_values(by=sort_column, ascending=False)
Out [26]:
| alpha:0.07 | alpha:0.1 | alpha:0.5 | alpha:1 | alpha:3 | |
|---|---|---|---|---|---|
| RM | 3.574162 | 3.414154 | 1.918419 | 0.938789 | 0.000000 |
| CHAS | 1.330724 | 0.979706 | 0.000000 | 0.000000 | 0.000000 |
| RAD | 0.278880 | 0.283443 | 0.300761 | 0.289299 | 0.146846 |
| ZN | 0.050107 | 0.050617 | 0.052878 | 0.052136 | 0.038268 |
| B | 0.010122 | 0.010067 | 0.009114 | 0.008320 | 0.007020 |
| AGE | -0.010116 | -0.008276 | 0.007760 | 0.020348 | 0.043446 |
| TAX | -0.014522 | -0.014814 | -0.016046 | -0.016218 | -0.011417 |
| INDUS | -0.044855 | -0.042719 | -0.023252 | -0.000000 | -0.000000 |
| CRIM | -0.099468 | -0.099213 | -0.089070 | -0.073577 | -0.019058 |
| NOX | -0.175072 | -0.000000 | -0.000000 | -0.000000 | -0.000000 |
| LSTAT | -0.574822 | -0.587702 | -0.693861 | -0.760457 | -0.800368 |
| PTRATIO | -0.779498 | -0.784725 | -0.790969 | -0.738672 | -0.423065 |
| DIS | -1.189438 | -1.173647 | -0.975902 | -0.725174 | -0.031208 |
선형 회귀 모델을 위한 데이터 변환
선형 회귀 모델은 피처값과 타깃값의 분포가 정규 분포 형태를 매우 선호한다.
선형 회귀 모델을 적용하기 전에 먼저 데이터에 대한 스케일링/정규화 작업을 수행하는 것이 일반적이다.
-
StandardScaler 클래스를 이용해 평균이 0, 분산이 1인 표준 정규 분포를 가진 데이터 세트로 변환하거나
MinMaxScaler 클래스를 이용해 최솟값이 0이고 최댓값이 1인 값으로 정규화를 수행 -
스케일링/정규화를 수행한 데이터 세트에 다시 다항 특성을 적용하여 변환. 보통 1번 방법을 통해 예측 성능에 향상이 없을 경우 이와 같은 방법을 적용
-
원래 값에 log 함수를 적용하면 보다 정규 분포에 가까운 형태로 값이 분포됨. 이러한 변환을 로그 변환(Log Transformation). 1,2번 보다 많이 사용됨.
In [27]:
from sklearn.preprocessing import StandardScaler, MinMaxScaler, PolynomialFeatures
In [28]:
# method는 표준 정규 분포 변환(Standard), 최대값/최소값 정규화(MinMax), 로그변환(Log) 결정
# p_degree는 다향식 특성을 추가할 때 적용. p_degree는 2이상 부여하지 않음.
def get_scaled_data(method='None', p_degree=None, input_data=None):
if method == 'Standard':
scaled_data = StandardScaler().fit_transform(input_data)
elif method == 'MinMax':
scaled_data = MinMaxScaler().fit_transform(input_data)
elif method == 'Log':
scaled_data = np.log1p(input_data)
else:
scaled_data = input_data
if p_degree != None:
scaled_data = PolynomialFeatures(degree=p_degree,
include_bias=False).fit_transform(scaled_data)
return scaled_data
In [29]:
alphas = [0.1, 1, 10, 100]
scale_methods = [(None, None), ('Standard', None), ('Standard', 2),
('MinMax', None), ('MinMax', 2), ('Log', None)]
for scale_method in scale_methods:
X_scaled_data = get_scaled_data(method=scale_method[0], p_degree=scale_method[1], input_data=X)
print(f'\n## 변환 유형: {scale_method[0]}, Polynomial Degree: {scale_method[1]}')
get_linear_reg_eval('Ridge', alphas, X_scaled_data, y, return_coeff=False)
Out [29]:
## 변환 유형: None, Polynomial Degree: None
####### Ridge #######
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.788
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.653
alpha 10일 때 5 폴드 세트의 평균 RMSE: 5.518
alpha 100일 때 5 폴드 세트의 평균 RMSE: 5.330
## 변환 유형: Standard, Polynomial Degree: None
####### Ridge #######
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.826
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.803
alpha 10일 때 5 폴드 세트의 평균 RMSE: 5.637
alpha 100일 때 5 폴드 세트의 평균 RMSE: 5.421
## 변환 유형: Standard, Polynomial Degree: 2
####### Ridge #######
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 8.827
alpha 1일 때 5 폴드 세트의 평균 RMSE: 6.871
alpha 10일 때 5 폴드 세트의 평균 RMSE: 5.485
alpha 100일 때 5 폴드 세트의 평균 RMSE: 4.634
## 변환 유형: MinMax, Polynomial Degree: None
####### Ridge #######
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.764
alpha 1일 때 5 폴드 세트의 평균 RMSE: 5.465
alpha 10일 때 5 폴드 세트의 평균 RMSE: 5.754
alpha 100일 때 5 폴드 세트의 평균 RMSE: 7.635
## 변환 유형: MinMax, Polynomial Degree: 2
####### Ridge #######
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 5.298
alpha 1일 때 5 폴드 세트의 평균 RMSE: 4.323
alpha 10일 때 5 폴드 세트의 평균 RMSE: 5.185
alpha 100일 때 5 폴드 세트의 평균 RMSE: 6.538
## 변환 유형: Log, Polynomial Degree: None
####### Ridge #######
alpha 0.1일 때 5 폴드 세트의 평균 RMSE: 4.770
alpha 1일 때 5 폴드 세트의 평균 RMSE: 4.676
alpha 10일 때 5 폴드 세트의 평균 RMSE: 4.836
alpha 100일 때 5 폴드 세트의 평균 RMSE: 6.241
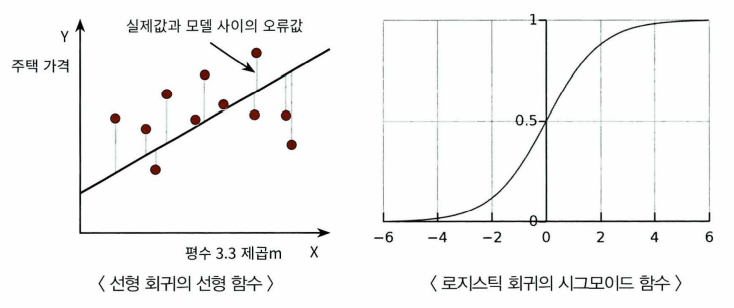
로지스틱 회귀
시그모이드(Sigmoid) 함수: 어떤 값이든 0~1사이의 값을 리턴
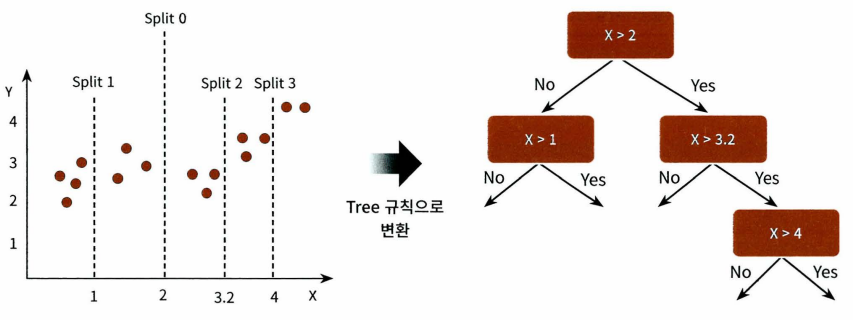
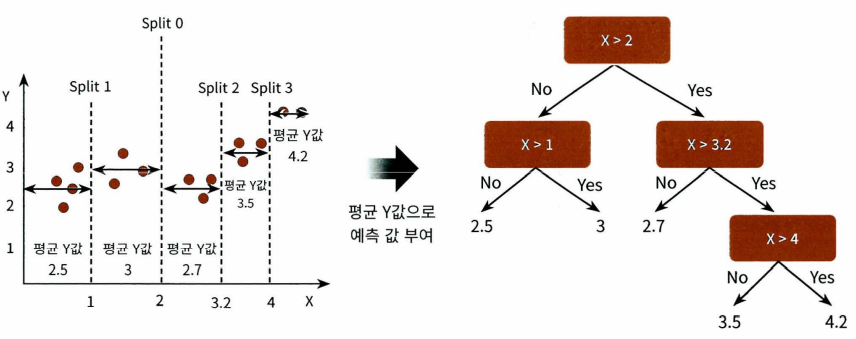
회귀 트리
회귀에 트리를 이용
Reference
- 이 포스트는 SeSAC 인공지능 자연어처리, 컴퓨터비전 기술을 활용한 응용 SW 개발자 양성 과정 - 심선조 강사님의 강의를 정리한 내용입니다.
댓글남기기