Data structure - Linear

---

자료 구조

선형 구조

순차 리스트

• Numpy array - 크기 고정, 동일한 자료형 저장 => 빠른 연산

각 요소로의 접근은 인덱스 번호로 가능하다.(print, search, update)
배열은 크기가 고정되어 있으므로 배열에 요소를 삽입하려면 먼저 증가된 크기(현재 크기 + 1)로 새 배열을 만들고 기존 요소를 복사한 다음 새 요소를 추가해야 한다. 축소된 크기의 새 배열로 삭제하는 경우에도 마찬가지이다.

• Python의 List - 크기 가변, 여러 자료형 저장 => 느린 연산

연결 리스트(Linked List)

노드(Node) - 연결된 목록의 각 요소
노드에는 key(값)와 다음 노드에 대한 포인터(주소)를 포함한다.
리스트 사이에 노드를 추가, 삭제가 용이하다.
하지만 특정 요소에 접근하기 위해서는 처음부터 순차적으로 탐색해야 하므로 배열에 비해 탐색속도가 떨어진다.

e.g)
사과, 딸기, 복숭아, 귤, 바나나
‘수박’을 딸기와 복숭아 사이에 넣기

일반 리스트의 경우
[사과, 딸기, 복숭아, 귤, 바나나]
바나나를 idx 5로, 귤을 idx 4로 복숭아를 idx 3으로 지정하고 수박을 idx 2로 지정

연결 리스트의 경우
사과-딸기-복숭아-귤-바나나
딸기 다음에 올 것이 수박으로 지정, 수박 다음에 올 것이 복숭아로 지정

• 단순 연결 리스트 (Singly Linked List)

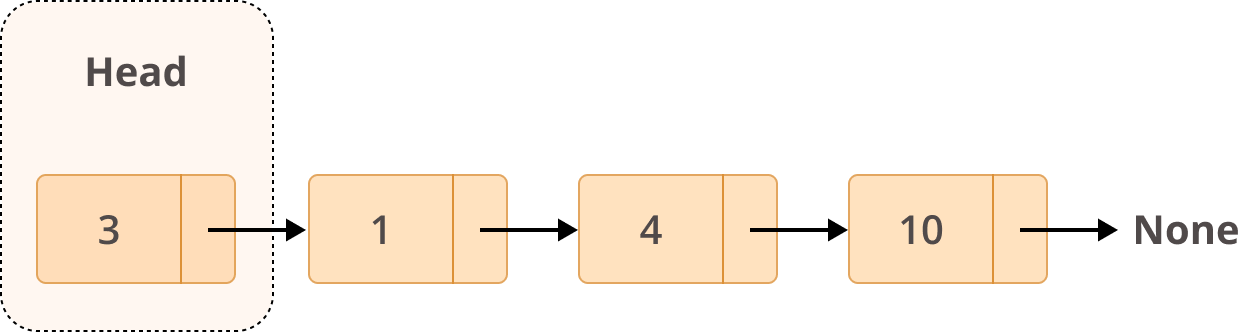
각 노드의 포인터가 다음 노드의 주소값을 가지고 있다.

• 이중 연결 리스트 (Doubly Linked List)

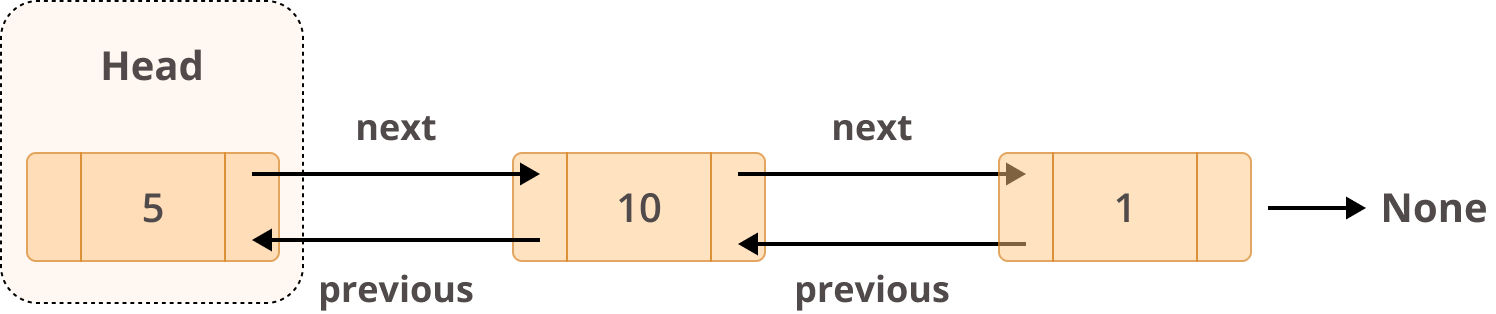
각 노드의 포인터가 다음 노드의 주소를 가리킬 뿐만 아니라 이전 노드의 주소도 가지고 있다.

• 원형 연결 리스트 (Circular linked list)

마지막 노드(tail)의 포인터가 NULL 대신 맨 처음 노드를 가리킨다.
이중 원형 연결 리스트의 구성도 가능하다.

스택(Stack)

LIFO (last-in-first-out);후입 선출

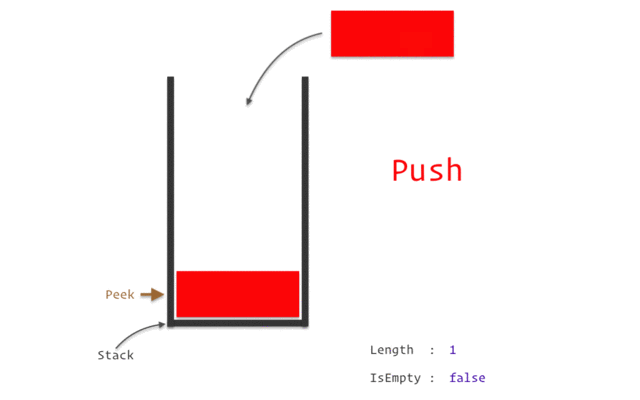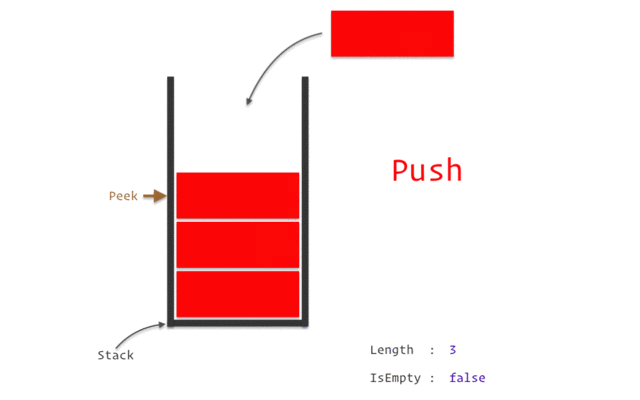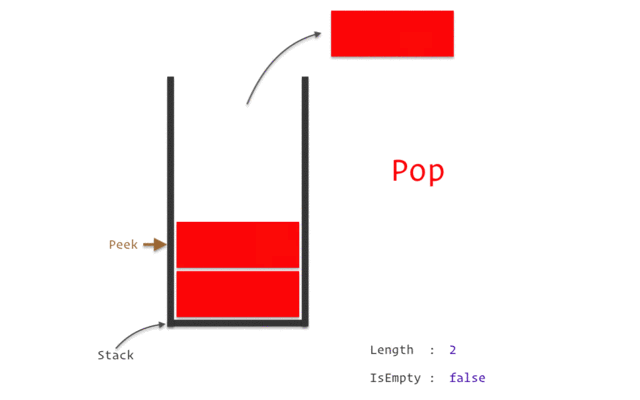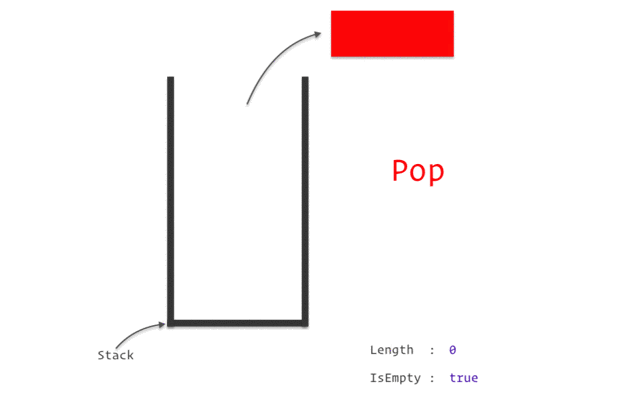
• top : 데이터가 들어올 공간
• stack.push: top에 새로운 데이터 삽입(top+1)
• stack.pop: 가장 최근에 push된 데이터를 삭제하고 반환(top-1)
• stack.peek: 가장 최근에 push된 데이터를 삭제하지 않고 반환
• stack.isEmpty: stack이 비어 있는지 확인(top==0)
• stack.isFull: stack이 꽉 찼는지 확인(top>stack_size)
• stack underflow: stack이 비어있을 때, stack.pop을 시도하는 것
• stack overflow: stack에 더이상 빈 공간이 없을 때, stack.push를 시도하는 것

재귀 알고리즘, DFS(Depth-first search;깊이 우선 탐색) 알고리즘, 작업 실행취소
괄호 검사, 문자열 역순 출력 등등

큐(Queue)

FIFO(first-in-first-out);선입 선출

• rear: 데이터가 들어갈 공간
• front: 데이터가 나갈 공간
• queue.enqueue: rear자리에 새로운 데이터 삽입(rear+1)
• queue.dequeue: front자리의 데이터를 삭제하고 반환(front+1)

front 앞에 공간이 남더라도 데이터를 삽입할 수 없다.

• 원형 큐(Circular Queue)

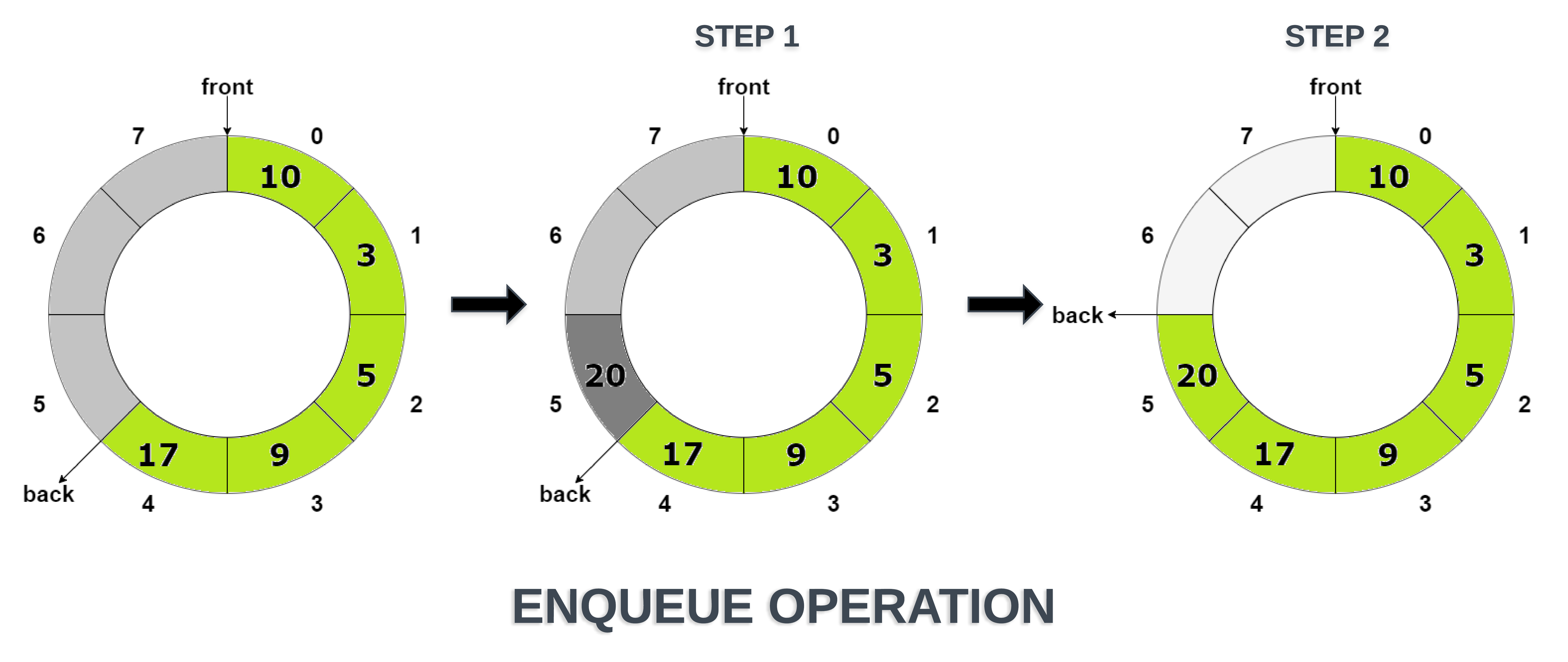
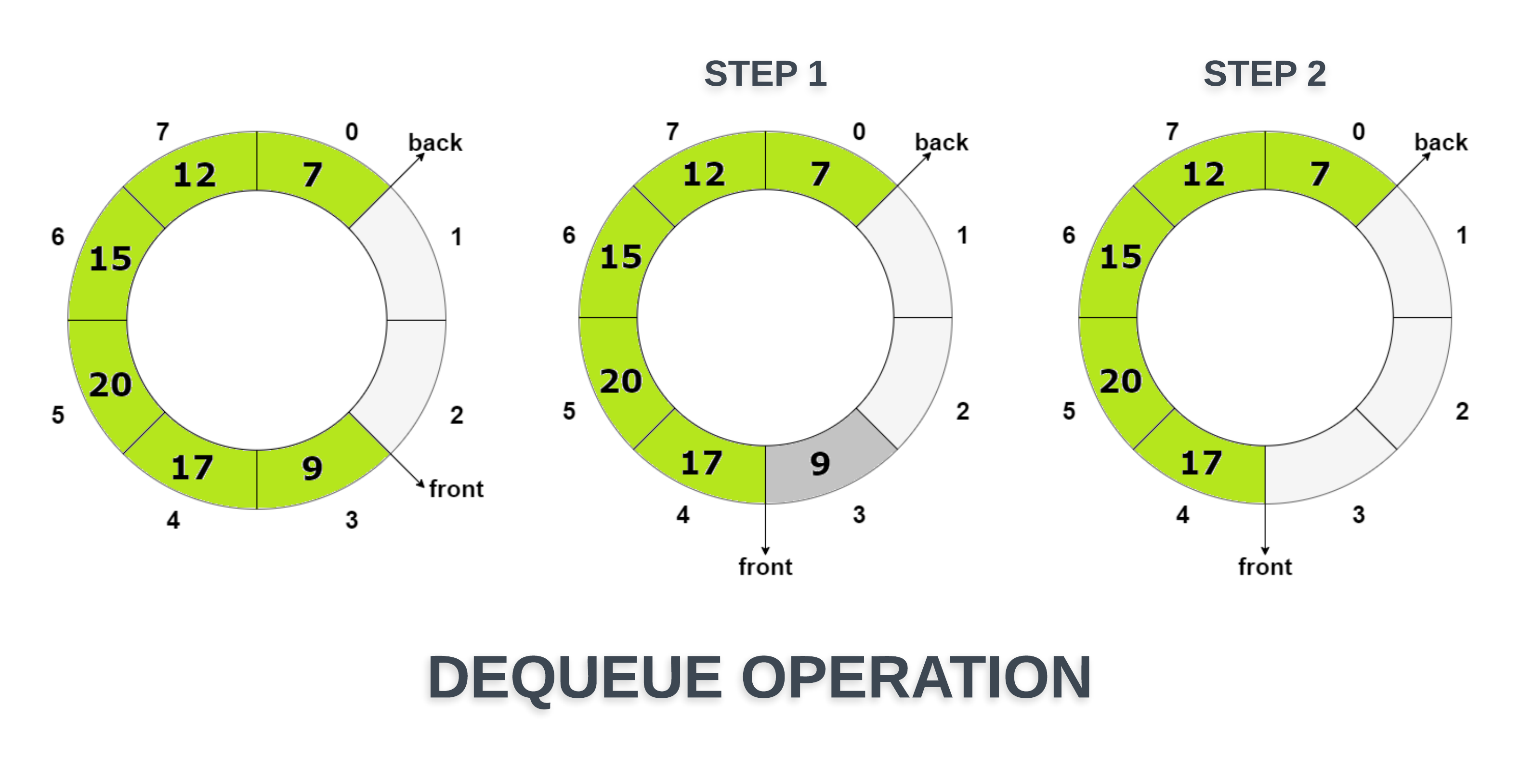
• queue.isEmpty: queue가 비어 있는지 확인(front==rear)
• queue.isFull: queue가 꽉 찼는지 확인(front==(rear+1)%queue_size)
• empty와 full을 구분하기 위해 queue의 공간 하나는 비우고 full로 생각한다.

BFS(Breadth-first search;너비 우선 탐색) 알고리즘, 프로세스(스레드) 관리
대기열 관리

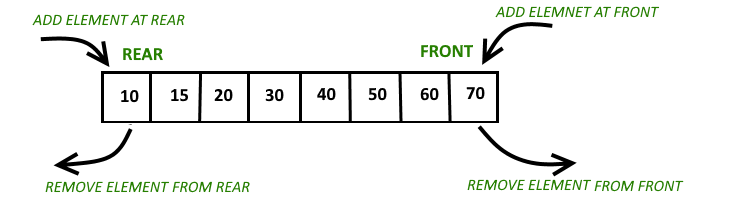
덱(Deque; Double ended queue)

양방향에서 push와 pop이 가능하다.

In [1]:

from collections import deque

d = deque()
d.append(10)
print(d)
d.append(20)
print(d)
d.appendleft(30)
print(d)
d.popleft()
print(d)
d.pop()
print(d)

Out [1]:

deque([10])
deque([10, 20])
deque([30, 10, 20])
deque([10, 20])
deque([10])

참고: List와 Deque의 시간복잡도

In [2]:

import time

def append_pop_timer(container, name):
    arr = range(10000000)
    
    start = time.time()
    for n in arr:
        container.append(arr)
    print(f'{name} append time: {time.time()-start:.3f} 초')
    
    start = time.time()
    for n in range(300):
        if type(container) is list:
            container.pop(0)
        else:
            container.popleft()
    print(f'{name} pop(0) time: {time.time()-start:.3f} 초')

lst = list()
dq = deque()

append_pop_timer(lst, 'list')
print()
append_pop_timer(dq, 'deque')

Out [2]:

list append time: 0.756 초
list pop(0) time: 6.512 초

deque append time: 0.504 초
deque pop(0) time: 0.000 초

Reference

• Vijini Mallawaarachchi: 8 Common Data Structures every Programmer must know
• Dhara Patel: JavaScript — Stacks and Queues
• 이유석: 자료구조
• python: TimeComplexity
• realpython: Linked Lists in Python: An Introduction
• AfterAcademy: Queue and its basic operations