Data structure - Non-linear

---

자료 구조

비선형 구조

그래프

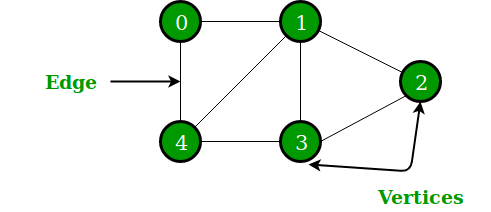
정점(vertix;node)과 간선(edge)으로 이루어진 자료 구조

가중치: 정점과 정점 사이에 드는 비용

그래프 표현

1. 인접 행렬(Adjacency Matrix): 2차원 배열로 그래프의 연결 관게를 표현하는 방식

In [1]:

INF = 999999999

graph = [
    [0, 7, 5],
    [7, 0, INF],
    [5, INF, 0]
]
print(graph)

Out [1]:

[[0, 7, 5], [7, 0, 999999999], [5, 999999999, 0]]

1. 인접 리스트(Adjacency List): 리스트로 그래프의 연결 관계를 표현하는 방식

In [2]:

graph = [
    [(1, 7), (2, 5)],
    [(0, 7)],
    [(0, 5)]
]
print(graph)

Out [2]:

[[(1, 7), (2, 5)], [(0, 7)], [(0, 5)]]

트리

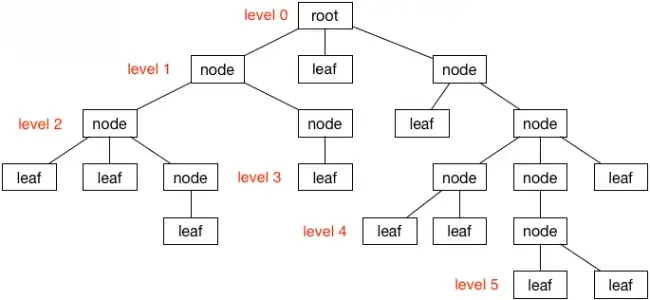
계층 구조를 가진 방향이 없는 그래프

• 노드(node): 트리를 구성하는 기본 원소
  • 루트 노드(root node/root): 트리에서 부모가 없는 최상위 노드, 트리의 시작점
  • 부모 노드(parent node): 루트 노드 방향으로 직접 연결된 노드
  • 자식 노드(child node): 루트 노드 반대방향으로 직접 연결된 노드
  • 형제 노드(siblings node): 같은 부모 노드를 갖는 노드들
  • 리프 노드(leaf node/leaf): 자식이 없는 노드(단말 노드)
• 간선(edge): 부모 노드와 자식 노드를 연결
• 차수(degree): 각 노드의 자식의 갯수

이진 트리

차수(degree)의 최댓값을 2로 제한한 트리

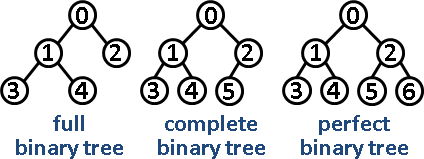
• 정 이진 트리(full binary tree): 각 내부의 노드가 두개의 자식노드를 가짐
• 완전 이진 트리(complete binary tree): 트리의 원소를 왼쪽에서 오른쪽으로 하나씩 빠짐없이 채워나간 형태
• 포화 이진 트리(perfect binary tree): 정 이진 트리이면서 완전 이진 트리인 경우

힙

힙은 항상 완전 이진 트리의 형태

• 부모의 값은 항상 자식들의 값보다 크다: Max heap;최대 힙
• 부모의 값은 항상 자식들의 값보다 작다: Min heap;최소 힙

루트노드에는 항상 데이터들 중 가장 큰or작은 값이 저장되어 있기 때문에, 최댓값or최솟값을 \(O(1)\)안에 찾을 수 있다.

Reference

• Vijini Mallawaarachchi: 8 Common Data Structures every Programmer must know
• Dhara Patel: JavaScript — Stacks and Queues
• 이유석: 자료구조
• python: TimeComplexity
• Christina: Understanding Binary Search Trees