Kwak Jisub

정리를 미루지 말자!

새싹 AI 프로그래머
화이팅!

2 분 소요

탐색 알고리즘

1. 리스트 - 순차 탐색

(Sequencial Search)

리스트의 특정 데이터를 찾기 위해 앞에서 부터 데이터를 하나씩 차례대로 확인하는 방법

In [13]: 
def sequential_search(arr, target, n):
    for i in range(n):
        if arr[i] == target:
            return i+1

arr = ['apple', 'orange', 'banana', 'grape', 'mango']
print('idx:', sequential_search(arr, 'banana', 5))
Out [13]: 
idx: 3

2. 리스트 - 이분 탐색

(Binary Search)

정렬된 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법

img

In [14]: 
# 재귀를 이용한 구현
def binary_search(arr, target, start, end):
    if start > end:
        return False
    mid = (start + end) // 2
    if arr[mid] == target:
        return mid
    elif arr[mid] > target:
        return binary_search(arr, target, start, mid-1)
    else:
        return binary_search(arr, target, mid+1, end)
    
arr = ['apple', 'orange', 'banana', 'grape', 'mango']
arr.sort()
print(arr)
rst = binary_search(arr, 'banana', 0, 5)
if rst == False:
    print('찾을 수 없습니다')
else:
    print('idx:', rst + 1)
Out [14]: 
['apple', 'banana', 'grape', 'mango', 'orange']
idx: 2
In [15]: 
# 반복문을 이용한 구현
def binary_search(arr, target, start, end):
    while start<= end:
        mid = (start + end) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] > target:
            end = mid - 1
        else:
            start = mid + 1
    return False

arr = ['apple', 'orange', 'banana', 'grape', 'mango']
arr.sort()
print(arr)
rst = binary_search(arr, 'banana', 0, 5)
if rst == False:
    print('찾을 수 없습니다')
else:
    print('idx:', rst + 1)
Out [15]: 
['apple', 'banana', 'grape', 'mango', 'orange']
idx: 2
  • 파이썬 내장 모듈 bisect
In [16]: 
from bisect import bisect_left, bisect_right
In [17]: 
arr = ['apple', 'banana', 'orange', 'banana', 'grape', 'mango']
arr.sort()
print(arr)

rst1 = bisect_left(arr, 'banana')
print('리스트중 맨 왼쪽 banana idx:', rst1)

rst2 = bisect_right(arr, 'banana')
print('리스트중 맨 오른쪽 banana 다음 idx:', rst2)

print('리스트에서 banana의 갯수:', rst2-rst1)
Out [17]: 
['apple', 'banana', 'banana', 'grape', 'mango', 'orange']
리스트중 맨 왼쪽 banana idx: 1
리스트중 맨 오른쪽 banana 다음 idx: 3
리스트에서 banana의 갯수: 2

3. 그래프 - 깊이 우선 탐색

(DFS; Depth First Search)

그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘

img

그림은 트리지만 그래프 형태에 사용한다.
DFS는 스택을 이용해서 구현한다.
단순 검색 속도 자체는 BFS보다 느리지만 순회(traversal)를 할 경우 사용된다.
백트래킹, 자동 미로 생성에 사용된다.

  1. 탐색 시작 노드를 스택에 삽입하고 방문처리(스택으로 한번 처리된 노드를 체크)
  2. 스택의 최상단 노드에 방문하지 않은 인접노드가 있으면 그 인접노드를 스택에 push하고 방문처리, 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 pop
  3. 2번 과정을 더 이상 수행할 수 없을 때까지 반복
In [18]: 
def dfs(graph, v, visited):
    # 방문처리
    visited[v] = True
    print(v, end=' → ')
    # 연결된 다른 노드를 방문
    for i in graph[v]:
        if not visited[i]:
            dfs(graph, i, visited)

img

In [19]: 
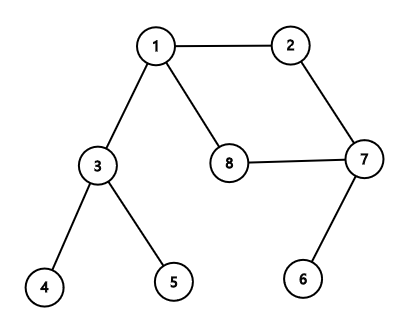
graph = [
    [],
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3],
    [3],
    [7],
    [2, 6, 8],
    [1, 7]
]
In [20]: 
visited = [False]*9
dfs(graph, 1, visited)
print('\b\b')
Out [20]: 
1 → 2 → 7 → 6 → 8 → 3 → 4 → 5

4. 그래프 - 너비 우선 검색

(BFS, Breadth First Search)

그래프에서 가까운 노드부터 탐색하는 알고리즘

img

BFS는 큐를 이용해서 구현한다.
일반적으로 실제 수행 시간은 DFS보다 좋은 편이다.
여러 갈래 중 무한한 길이를 가지는 경로가 존재하고 탐색 목표가 다른 경로에 존재하는 경우 DFS로 탐색할 시에는 무한한 길이의 경로에서 영원히 종료하지 못하지만, BFS의 경우는 모든 경로를 동시에 진행하기 때문에 탐색이 가능하다.

  1. 탐색 시작 노드를 큐에 삽입하고 방문처리(스택으로 한번 처리된 노드를 체크)
  2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문처리
  3. 2번 과정을 더 이상 수행할 수 없을 때까지 반복
In [21]: 
from collections import deque
In [22]: 
def bfs(graph, start, visited):
    # 시작지점을 queue에 넣음
    queue = deque([start])
    # 방문처리
    visited[start] = True
    while queue: # queue가 빌 때까지
        v = queue.popleft()
        print(v, end=' → ')
        # 연결된 방문하지 않은 노드를 큐에 enqueue
        for i in graph[v]:
            if not visited[i]:
                queue.append(i)
                visited[i] = True

img

In [23]: 
graph = [
    [],
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3],
    [3],
    [7],
    [2, 6, 8],
    [1, 7]
]
In [24]: 
visited = [False]*9
bfs(graph, 1, visited)
print('\b\b')
Out [24]: 
1 → 2 → 3 → 8 → 7 → 4 → 5 → 6

Reference

댓글남기기

참고