Numpy (1)
Numpy 가져오기
NumPy(Numerical Python)는 거의 모든 과학 및 공학 분야에서 사용되는 오픈 소스 Python 라이브러리이다. Python에서 숫자 데이터로 작업할 때의 보편적인 표준이고 과학적 Python 및 PyData 생태계의 핵심이다. NumPy 사용자는 초급 코더에서부터 최첨단 과학, 연구 및 개발 산업 분야의 경험이 풍부한 연구원까지 모든 사람을 포함한다. NumPy API는 Pandas, SciPy, Matplotlib, scikit-learn, scikit-image 그리고 기타 대부분의 데이터 사이언스, 과학적 Python 패키지에서 널리 사용되고 있다.
In [1]:
import numpy as np
In [2]:
np.__version__
Out [2]:
'1.21.5'
Numpy 예제
In [3]:
# range array 생성
a = np.arange(6)
a
Out [3]:
array([0, 1, 2, 3, 4, 5])
In [4]:
a2 = a[np.newaxis, :]
a2
Out [4]:
array([[0, 1, 2, 3, 4, 5]])
In [5]:
a2.shape
Out [5]:
(1, 6)
Numpy array와 Python list의 차이
Numpy array의 모든 요소는 데이터 타입이 같아야 한다. array에 대해 수행되는 수학 연산은 array의 요소의 데이터 타입이 다를 경우 극도로 비효율적이다.
Python list보다 빠르고 컴팩트하다. Array는 메모리가 적고 사용하기 편리하다. Numpy는 데이터를 저장하는 데 훨씬 적은 메모리를 사용한다. 데이터 유형을 지정하는 메커니즘을 제공한다. 이를 통해 코드를 더욱 최적화 할 수 있다.
Array란?
Array란 Numpy 라이브러리의 중심 데이터 구조이다.
In [6]:
# array 생성
a = np.array([1, 2, 3, 4, 5, 6])
In [7]:
# 통일된 array element의 데이터 타입 보기
a.dtype
Out [7]:
dtype('int32')
In [8]:
# 다른 타입을 넣을 경우 하나로 통일시킴
a = np.array([1., 2, 3, 4, 5, 6])
a.dtype
Out [8]:
dtype('float64')
In [9]:
a = np.array(['1', 2, 3, 4, 5, 6])
a.dtype
Out [9]:
dtype('<U11')
In [10]:
# 속성(attribute)호출 : ()없음
# 메서드 호출 : ()있음
a.ndim # number of array dimensions
Out [10]:
1
In [11]:
# shape : integer형태의 tuple로 각 dimension의 크기를 나타냄
a.shape
Out [11]:
(6,)
In [12]:
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
a.dtype
Out [12]:
dtype('int32')
In [13]:
a.ndim
Out [13]:
2
In [14]:
a.shape
Out [14]:
(3, 4)
In [15]:
a
Out [15]:
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
In [16]:
print(a)
Out [16]:
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
In [17]:
a[0, 3]
Out [17]:
4
In [18]:
a[:, 3]
Out [18]:
array([ 4, 8, 12])
- scalar : 단일 element
- vector : 단일 차원의 array
- matrix : 2차원 array
- tensor : 3차원 이상의 array
기본 array 만드는 법
In [19]:
np.array([[1,2],[3,4],[5,6]])
Out [19]:
array([[1, 2],
[3, 4],
[5, 6]])
In [20]:
np.array([[[1,2],[3,4],[5,6]],[[1,2],[3,4],[5,6]]])
Out [20]:
array([[[1, 2],
[3, 4],
[5, 6]],
[[1, 2],
[3, 4],
[5, 6]]])
In [21]:
# 데이터 갯수가 다를 경우 list로 쪼개짐
np.array([[[1,2],[3,4],[5,6]],[[1,2],[3,4],[5,6,7]]])
Out [21]:
C:\Users\user\AppData\Local\Temp\ipykernel_15108\1008207123.py:2: VisibleDeprecationWarning: Creating an ndarray from ragged nested sequences (which is a list-or-tuple of lists-or-tuples-or ndarrays with different lengths or shapes) is deprecated. If you meant to do this, you must specify 'dtype=object' when creating the ndarray.
np.array([[[1,2],[3,4],[5,6]],[[1,2],[3,4],[5,6,7]]])
array([[list([1, 2]), list([3, 4]), list([5, 6])],
[list([1, 2]), list([3, 4]), list([5, 6, 7])]], dtype=object)
In [22]:
# 0으로 초기값을 지정하고 싶을 경우
np.zeros((2,3)) # np.zeros(shape, dtype=float, order='C', *, like=None)
Out [22]:
array([[0., 0., 0.],
[0., 0., 0.]])
In [23]:
# 1로 초기값을 지정하고 싶을 경우
np.ones((2,3)) # np.ones(shape, dtype=None, order='C', *, like=None)
Out [23]:
array([[1., 1., 1.],
[1., 1., 1.]])
In [24]:
# 초기값이 무작위, 메모리상태에 따라 달라짐 (초기화하는 과정을 하지 않으므로 속도가 쪼금 빠름)
np.empty((2,3)) # np.empty(shape, dtype=float, order='C', *, like=None)
Out [24]:
array([[1., 1., 1.],
[1., 1., 1.]])
In [25]:
np.arange(6) # np.arange([start,] stop[, step,], dtype=None, *, like=None)
Out [25]:
array([0, 1, 2, 3, 4, 5])
In [26]:
# 시작값과 끝값 사이에 일정 갯수를 균등 간격으로 지정하고 싶을 경우
np.linspace(0, 10, num=5) # np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)
# parameter는 순서대로 넣을 경우 생략가능, 아닐경우 명시.
Out [26]:
array([ 0. , 2.5, 5. , 7.5, 10. ])
In [27]:
# 데이터 유형 지정
np.zeros((2,3), dtype=np.int8) # int8 ~ int64 : 1바이트 ~ 8바이트로 표현하는 int. 적절한 data의 크기를 잡아줘야 한다. default는 64
Out [27]:
array([[0, 0, 0],
[0, 0, 0]], dtype=int8)
Element의 정렬과 추가
np.sort()
In [28]:
arr = np.array([2, 1, 5, 3, 7, 4, 6, 8])
In [29]:
np.sort(arr) # np.sort(a, axis=-1, kind=None, order=None) # axis는 정렬할 기준(-1은 끝값, 차원이 늘어도 무조건 열이 기준이 됨)
Out [29]:
array([1, 2, 3, 4, 5, 6, 7, 8])
In [30]:
# 내림차순이 필요한 경우
np.sort(arr)[::-1] # 처음부터:끝까지:역순
Out [30]:
array([8, 7, 6, 5, 4, 3, 2, 1])
In [31]:
# 2차원 정렬
a = np.array([[1,4],[3,1]])
a
Out [31]:
array([[1, 4],
[3, 1]])
In [32]:
np.sort(a)
# default인 axis=-1는 shape에서 나온 2x2에서 -1(끝)인 열기준(column을 묶어 정렬 --방향)
Out [32]:
array([[1, 4],
[1, 3]])
In [33]:
np.sort(a, axis=1)
Out [33]:
array([[1, 4],
[1, 3]])
In [34]:
np.sort(a, axis=0)
# axis=0은 2x2에서 0인 행기준(row를 묶어 정렬 |방향)
Out [34]:
array([[1, 1],
[3, 4]])
-
argsort: 지정된 축을 따른 간접 정렬
-
lexsort: 여러 키에 대한 간접 안정 정렬
-
searchsorted: 정렬된 array에서 element 찾기
-
partition: 부분 정렬
np.argsort()
In [35]:
x = np.array([3, 1, 2])
In [36]:
# 인덱스 값을 리턴
np.argsort(x) # np.argsort(a, axis=-1, kind=None, order=None)
Out [36]:
array([1, 2, 0], dtype=int64)
In [37]:
np.argmax(x) # 딥러닝에서 사용 # arg가 붙은 함수는 idx를 리턴한다!
Out [37]:
0
In [38]:
# 2차원일 경우
x = np.array([[0, 3], [2, 2]])
x
Out [38]:
array([[0, 3],
[2, 2]])
In [39]:
np.argsort(x, axis=-1)
Out [39]:
array([[0, 1],
[0, 1]], dtype=int64)
In [40]:
np.argsort(x, axis=1)
Out [40]:
array([[0, 1],
[0, 1]], dtype=int64)
In [41]:
np.argsort(x, axis=0)
Out [41]:
array([[0, 1],
[1, 0]], dtype=int64)
np.concatenate()
In [42]:
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
In [43]:
np.concatenate((a, b)) # concatenate((a1, a2, ...), axis=0, out=None, dtype=None, casting="same_kind")
Out [43]:
array([1, 2, 3, 4, 5, 6, 7, 8])
In [44]:
# 2차원일 경우
a = np.array([[1, 2, 3, 4]])
b = np.array([[5, 6, 7, 8]])
In [45]:
np.concatenate((a, b), axis=0)
Out [45]:
array([[1, 2, 3, 4],
[5, 6, 7, 8]])
In [46]:
np.concatenate((a, b), axis=1)
Out [46]:
array([[1, 2, 3, 4, 5, 6, 7, 8]])
In [47]:
# 3차원일 경우
a = np.array([[[1, 2, 3, 4]]])
b = np.array([[[5, 6, 7, 8]]])
In [48]:
np.concatenate((a, b), axis=0)
Out [48]:
array([[[1, 2, 3, 4]],
[[5, 6, 7, 8]]])
In [49]:
np.concatenate((a, b), axis=1)
Out [49]:
array([[[1, 2, 3, 4],
[5, 6, 7, 8]]])
In [50]:
np.concatenate((a, b), axis=2)
Out [50]:
array([[[1, 2, 3, 4, 5, 6, 7, 8]]])
Array의 모양과 크기
In [51]:
# axes or dimensions
a.ndim
Out [51]:
3
In [52]:
# 각 dimension에 몇개의 element가 있는지
a.shape
Out [52]:
(1, 1, 4)
In [53]:
# element의 총 갯수
a.size
Out [53]:
4
In [54]:
np.concatenate((a, b), axis=0).shape # method chaining
Out [54]:
(2, 1, 4)
Array의 reshape
In [55]:
a = np.arange(6)
a
Out [55]:
array([0, 1, 2, 3, 4, 5])
In [56]:
# array의 데이터를 변경하지 않고 모양을 변경
a.reshape(3, 2) # .reshape(shape, order='C')
Out [56]:
array([[0, 1],
[2, 3],
[4, 5]])
In [57]:
a.reshape(2, 3)
Out [57]:
array([[0, 1, 2],
[3, 4, 5]])
In [58]:
np.reshape(a, (2, 3)) # np.reshape(a, newshape, order='C')
Out [58]:
array([[0, 1, 2],
[3, 4, 5]])
Array에 새 axis 추가
np.newaxis
In [59]:
a = np.array([1, 2, 3, 4, 5, 6])
a.shape
Out [59]:
(6,)
In [60]:
a2 = a[np.newaxis, :]
a2
Out [60]:
array([[1, 2, 3, 4, 5, 6]])
In [61]:
a2.shape
Out [61]:
(1, 6)
In [62]:
a3 = a[:, np.newaxis]
a3
Out [62]:
array([[1],
[2],
[3],
[4],
[5],
[6]])
In [63]:
a3.shape
Out [63]:
(6, 1)
np.expand_dims()
In [64]:
b = np.expand_dims(a, axis=0) # np.expand_dims(a, axis) # axis에 어디에 차원을 늘릴지 지정 가능
b
Out [64]:
array([[1, 2, 3, 4, 5, 6]])
In [65]:
b2 = np.expand_dims(a, axis=1)
b2
Out [65]:
array([[1],
[2],
[3],
[4],
[5],
[6]])
In [66]:
# 2차원일 경우
aa = a3.reshape((3, 2))
aa
Out [66]:
array([[1, 2],
[3, 4],
[5, 6]])
In [67]:
a4 = np.expand_dims(aa, axis=0)
a4.shape
Out [67]:
(1, 3, 2)
In [68]:
a4 = np.expand_dims(aa, axis=1)
a4.shape
Out [68]:
(3, 1, 2)
In [69]:
a4 = np.expand_dims(aa, axis=2)
a4.shape
Out [69]:
(3, 2, 1)
Indexing과 slicing
In [70]:
data = np.array([1, 2, 3])
In [71]:
data[1]
Out [71]:
2
In [72]:
data[0:2]
Out [72]:
array([1, 2])
In [73]:
data[1:]
Out [73]:
array([2, 3])
In [74]:
data[-2:]
Out [74]:
array([2, 3])
조건추가
In [75]:
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
a
Out [75]:
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
In [76]:
print("a.ndim: {}, a.shape: {}".format(a.ndim, a.shape))
Out [76]:
a.ndim: 2, a.shape: (3, 4)
In [77]:
a[a>=5]
Out [77]:
array([ 5, 6, 7, 8, 9, 10, 11, 12])
In [78]:
a[a%2==0]
Out [78]:
array([ 2, 4, 6, 8, 10, 12])
In [79]:
a[(a>2) & (a<11)] # 모호성 때문에 연산자 우선순위가 있더라도 괄호로 명확히 해야함
Out [79]:
array([ 3, 4, 5, 6, 7, 8, 9, 10])
In [80]:
a[(a>5) | (a==5)]
Out [80]:
array([ 5, 6, 7, 8, 9, 10, 11, 12])
In [81]:
b = np.nonzero(a<5) # 조건에 맞는 행열값을 리턴 (각 차원에 대해 하나씩 array의 tuple이 리턴된다)
b
Out [81]:
(array([0, 0, 0, 0], dtype=int64), array([0, 1, 2, 3], dtype=int64))
In [82]:
list(zip(b[0], b[1])) # zip: 같은 위치의 값을 묶어줌, 보통 list와 같이 사용
Out [82]:
[(0, 0), (0, 1), (0, 2), (0, 3)]
기존 데이터로 array 만들기
In [83]:
a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
In [84]:
# view 생성
arr1 = a[3:8] # 값을 복사하는 것이 아니라 참조를 하고 있기에 이 array을 변경하면 원 array도 바뀐다!(얕은 복사)
arr1
Out [84]:
array([4, 5, 6, 7, 8])
In [85]:
a
Out [85]:
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
In [86]:
arr1[0] = 14
In [87]:
a
Out [87]:
array([ 1, 2, 3, 14, 5, 6, 7, 8, 9, 10])
In [88]:
a1 = np.array([[1, 1],
[2, 2]])
a2 = np.array([[3, 3],
[4, 4]])
# 위아래로 붙이려면 열이 맞아야 하고 좌우로 붙이려면 행이 맞아야 한다
In [89]:
np.concatenate((a1, a2), axis=1)
Out [89]:
array([[1, 1, 3, 3],
[2, 2, 4, 4]])
In [90]:
# vertical 쌓기
np.vstack((a1, a2))
Out [90]:
array([[1, 1],
[2, 2],
[3, 3],
[4, 4]])
In [91]:
# horizontal 쌓기
np.hstack((a1, a2))
Out [91]:
array([[1, 1, 3, 3],
[2, 2, 4, 4]])
In [92]:
# horizontal 분리(수평으로 된 것을 분리: |로 자름)
x = np.arange(1, 25).reshape(2, 12)
x
Out [92]:
array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12],
[13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]])
In [93]:
np.hsplit(x, 3)
Out [93]:
[array([[ 1, 2, 3, 4],
[13, 14, 15, 16]]),
array([[ 5, 6, 7, 8],
[17, 18, 19, 20]]),
array([[ 9, 10, 11, 12],
[21, 22, 23, 24]])]
In [94]:
np.hsplit(x, (3, 4)) # idx 3과 4앞에서 자름
Out [94]:
[array([[ 1, 2, 3],
[13, 14, 15]]),
array([[ 4],
[16]]),
array([[ 5, 6, 7, 8, 9, 10, 11, 12],
[17, 18, 19, 20, 21, 22, 23, 24]])]
- 얕은 복사(슬라이싱)가 아닌 원본을 두고 복사본 생성 : copy()
In [95]:
b2 = a.copy()
print(a)
print(b2)
Out [95]:
[ 1 2 3 14 5 6 7 8 9 10]
[ 1 2 3 14 5 6 7 8 9 10]
In [96]:
b2[3] = 4
print(a)
print(b2)
Out [96]:
[ 1 2 3 14 5 6 7 8 9 10]
[ 1 2 3 4 5 6 7 8 9 10]
기본 array 연산
In [97]:
data = np.array([1, 2])
ones = np.ones(2, dtype=int)
print(data)
print(ones)
Out [97]:
[1 2]
[1 1]
In [98]:
data + ones
Out [98]:
array([2, 3])
In [99]:
data - ones
Out [99]:
array([0, 1])
In [100]:
data * data
Out [100]:
array([1, 4])
In [101]:
data / data
Out [101]:
array([1., 1.])
In [102]:
a = np.array([1, 2, 3, 4])
a.sum()
Out [102]:
10
In [103]:
b = np.array([[1, 1], [2, 2]])
b.sum() # .sum(axis=None, dtype=None, out=None, keepdims=False, initial=0, where=True)
Out [103]:
6
In [104]:
b
Out [104]:
array([[1, 1],
[2, 2]])
In [105]:
b.sum(0) # axis=0
Out [105]:
array([3, 3])
In [106]:
b.sum(1)
Out [106]:
array([2, 4])
Broadcast
- array와 단일 숫자 사이의 연산(벡터와 스칼라 간의 연산이라고도 함) 또는 두 개의 서로 다른 크기의 array 간에 연산을 수행
In [107]:
data = np.array([1.0, 2.0])
data
Out [107]:
array([1., 2.])
In [108]:
data * 1.6 # 1.6(스칼라;scalar값)이 확장 [1.6, 1.6] 하여 연산된다
Out [108]:
array([1.6, 3.2])
일반 broadcast 규칙
- 두 개의 array에서 작업할 때 Numpy는 element 별로 모양을 비교한다. 후행(즉, 맨 오른쪽) 차원에서 시작하여 왼쪽으로 작동한다.
- 두 차원은 다음과 같은 경우 호환된다.
- 같을 때
- 그 중 하나가 1일 때
- 이러한 조건이 충족되지 않으면 array에 호환되지 않는 모양이 있음을 나타내는 예외가 발생
(ValueError: operands could not be broadcast together)
In [109]:
a = np.array([[ 0.0, 0.0, 0.0],
[10.0, 10.0, 10.0],
[20.0, 20.0, 20.0],
[30.0, 30.0, 30.0]])
a.shape
Out [109]:
(4, 3)
In [110]:
b = np.array([1.0, 2.0, 3.0])
b.shape
Out [110]:
(3,)
In [111]:
a + b
Out [111]:
array([[ 1., 2., 3.],
[11., 12., 13.],
[21., 22., 23.],
[31., 32., 33.]])
In [112]:
c = np.array([8])
c.shape
Out [112]:
(1,)
In [113]:
a * c
Out [113]:
array([[ 0., 0., 0.],
[ 80., 80., 80.],
[160., 160., 160.],
[240., 240., 240.]])
유용한 array 연산
In [114]:
data
Out [114]:
array([1., 2.])
In [115]:
data.max()
Out [115]:
2.0
In [116]:
data.min()
Out [116]:
1.0
In [117]:
data.sum()
Out [117]:
3.0
Matrix(행렬) 생성
In [118]:
data = np.array([[1, 2], [3, 4], [5, 6]])
data
Out [118]:
array([[1, 2],
[3, 4],
[5, 6]])
Random number 생성
In [119]:
rng = np.random.default_rng(1) # seed값이 같으면 같은 값이 나온다!
In [120]:
rng.random(3)
Out [120]:
array([0.51182162, 0.9504637 , 0.14415961])
In [121]:
rng.integers(1, 5) # integers(low, high=None, size=None, dtype=np.int64, endpoint=False)
Out [121]:
4
In [122]:
rng.integers(1, 5, endpoint=True)
Out [122]:
5
Unique items와 count
In [123]:
a = np.array([11, 11, 12, 13, 14, 15, 16, 17, 12, 13, 11, 14, 18, 19, 20])
a
Out [123]:
array([11, 11, 12, 13, 14, 15, 16, 17, 12, 13, 11, 14, 18, 19, 20])
In [124]:
np.unique(a, return_index=True) # np.unique(ar, return_index=False, return_inverse=False, return_counts=False, axis=None)
Out [124]:
(array([11, 12, 13, 14, 15, 16, 17, 18, 19, 20]),
array([ 0, 2, 3, 4, 5, 6, 7, 12, 13, 14], dtype=int64))
In [125]:
np.unique(a, return_inverse=True) # inverse는 원본 array의 값을 return된 array의 값에 해당하는 index값을 표시
Out [125]:
(array([11, 12, 13, 14, 15, 16, 17, 18, 19, 20]),
array([0, 0, 1, 2, 3, 4, 5, 6, 1, 2, 0, 3, 7, 8, 9], dtype=int64))
In [126]:
np.unique(a, return_counts=True) # 중복 count
Out [126]:
(array([11, 12, 13, 14, 15, 16, 17, 18, 19, 20]),
array([3, 2, 2, 2, 1, 1, 1, 1, 1, 1], dtype=int64))
Matrix의 transposing과 reshaping
In [127]:
data = np.arange(1, 7).reshape(2, 3)
data
Out [127]:
array([[1, 2, 3],
[4, 5, 6]])
In [128]:
# 행과 열을 바꿈
data.transpose()
Out [128]:
array([[1, 4],
[2, 5],
[3, 6]])
In [129]:
data.T
Out [129]:
array([[1, 4],
[2, 5],
[3, 6]])
Array 뒤집기
In [130]:
arr = np.array([1, 2, 3, 4, 9, 5, 6, 7, 8])
arr
Out [130]:
array([1, 2, 3, 4, 9, 5, 6, 7, 8])
In [131]:
np.flip(arr)
Out [131]:
array([8, 7, 6, 5, 9, 4, 3, 2, 1])
In [132]:
# 2차원의 경우
arr_2d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
arr_2d
Out [132]:
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
In [133]:
np.flip(arr_2d)
Out [133]:
array([[12, 11, 10, 9],
[ 8, 7, 6, 5],
[ 4, 3, 2, 1]])
In [134]:
np.flip(arr_2d, axis=0) # 행만 뒤집음
Out [134]:
array([[ 9, 10, 11, 12],
[ 5, 6, 7, 8],
[ 1, 2, 3, 4]])
In [135]:
np.flip(arr_2d, axis=1) # 열만 뒤집음
Out [135]:
array([[ 4, 3, 2, 1],
[ 8, 7, 6, 5],
[12, 11, 10, 9]])
다차원 array의 reshaping과 flattening
- .flatten() : 1차원으로 평탄화
- .ravel() : 1차원으로 평탄화, 복사본을 생성하지 않으므로 메모리 효율적(얕은 복사)
In [136]:
x = np.array([[1 , 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
x
Out [136]:
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
In [137]:
x.flatten()
Out [137]:
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
In [138]:
x.reshape((1, -1))[0] # 같은 효과이나 번거로움
Out [138]:
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
Docstring
In [139]:
x.reshape?
# Shift + tab이 편함...
Out [139]:
[1;31mDocstring:[0m
a.reshape(shape, order='C')
Returns an array containing the same data with a new shape.
Refer to `numpy.reshape` for full documentation.
See Also
--------
numpy.reshape : equivalent function
Notes
-----
Unlike the free function `numpy.reshape`, this method on `ndarray` allows
the elements of the shape parameter to be passed in as separate arguments.
For example, ``a.reshape(10, 11)`` is equivalent to
``a.reshape((10, 11))``.
[1;31mType:[0m builtin_function_or_method
In [140]:
def double(a):
'''
docstring 내용
double(arr)
'''
return a * 2
In [141]:
double?
Out [141]:
[1;31mSignature:[0m [0mdouble[0m[1;33m([0m[0ma[0m[1;33m)[0m[1;33m[0m[1;33m[0m[0m
[1;31mDocstring:[0m
docstring 내용
double(arr)
[1;31mFile:[0m c:\users\user\appdata\local\temp\ipykernel_15108\354467443.py
[1;31mType:[0m function
In [142]:
double??
# 사용자 함수는 소스도 함께 표시
Out [142]:
[1;31mSignature:[0m [0mdouble[0m[1;33m([0m[0ma[0m[1;33m)[0m[1;33m[0m[1;33m[0m[0m
[1;31mSource:[0m
[1;32mdef[0m [0mdouble[0m[1;33m([0m[0ma[0m[1;33m)[0m[1;33m:[0m[1;33m
[0m [1;34m'''
docstring 내용
double(arr)
'''[0m[1;33m
[0m [1;32mreturn[0m [0ma[0m [1;33m*[0m [1;36m2[0m[1;33m[0m[1;33m[0m[0m
[1;31mFile:[0m c:\users\user\appdata\local\temp\ipykernel_15108\354467443.py
[1;31mType:[0m function
수학 공식 사용
-
Array에서 작동하는 수학 공식을 쉽게 구현할 수 있다는 것이 Numpy가 과학적 Python 커뮤니티에서 널리 사용되는 이유이다.
-
다음은 평균 제곱 오차 공식(mean square error formula)이다. 회귀를 다루는 지도 머신 러닝 모델에서 사용하는 중심 공식이다.
- Y_prediction: 예측값
- Y: 정답값
Numpy 객체 저장, 불러오기
In [143]:
# np.save('filename', a) # filename.npy로 저장
In [144]:
# b = np.load('filename.npy')
In [145]:
# np.savetxt('new_file.csv', csv_arr) # csv로 저장
In [146]:
# np.loadtxt('new_file.csv')
Reference
- 이 포스트는 SeSAC 인공지능 SW 개발자 양성 과정 - 심선조 강사님의 강의내용을 정리한 것입니다.
- NumPy.org : NumPy
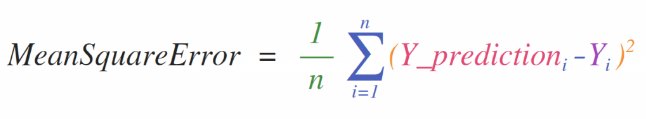
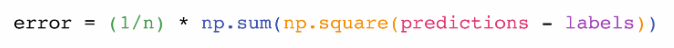
댓글남기기