Numpy (2)

2022년 11월 15일 4 분 소요

N차원 배열의 선형 대수학

Numpy에서 1차원, 2차원 및 n차원 배열의 차이점을 이해
for 루프를 사용하지 않고 n차원 배열에 일부 선형 대수 연산을 적용하는 방법을 이해
n차원 배열의 axis 및 shape 속성을 이해

In [1]:

# scipy.misc 모듈 의 face이미지를 사용
from scipy import misc

In [2]:

img = misc.face()

데이터 shape, axis, array 정보

In [3]:

img.ndim

Out [3]:

In [4]:

# (세로, 가로, rgb)
img.shape

Out [4]:

(768, 1024, 3)

In [5]:

# element의 수
img.size

Out [5]:

In [6]:

img.dtype

Out [6]:

dtype('uint8')

In [7]:

type(img)

Out [7]:

numpy.ndarray

In [8]:

# 첫 픽셀의 rgb의 범위 출력
img[0, 0, :]

Out [8]:

array([121, 112, 131], dtype=uint8)

In [9]:

print("값의 범위 : {} ~ {}".format(img.min(), img.max()))

Out [9]:

값의 범위 : 0 ~ 255

In [10]:

import matplotlib.pyplot as plt
# %matplotlib inline 예전버전에서 이미지가 나오지 않을 경우 사용

In [11]:

plt.imshow(img)
plt.show() # imshow와 show 같은 cell에 사용

Out [11]:

In [12]:

# r값 출력
img[:, :, 0]

Out [12]:

array([[121, 138, 153, ..., 119, 131, 139],
       [ 89, 110, 130, ..., 118, 134, 146],
       [ 73,  94, 115, ..., 117, 133, 144],
       ...,
       [ 87,  94, 107, ..., 120, 119, 119],
       [ 85,  95, 112, ..., 121, 120, 120],
       [ 85,  97, 111, ..., 120, 119, 118]], dtype=uint8)

In [13]:

# g값 출력
img[:, :, 1]

Out [13]:

array([[112, 129, 144, ..., 126, 136, 144],
       [ 82, 103, 122, ..., 125, 141, 153],
       [ 66,  87, 108, ..., 126, 142, 153],
       ...,
       [106, 110, 124, ..., 158, 157, 158],
       [101, 111, 127, ..., 157, 156, 156],
       [101, 113, 126, ..., 156, 155, 154]], dtype=uint8)

In [14]:

# img size 확인
img[:, :, 0].shape

Out [14]:

(768, 1024)

0 - 255 이면 값의 차이가 크므로 0 - 1로 조정

차이가 크면 작은 값들의 중요도가 무시될 수 있기에

In [15]:

img_array = img / 255

In [16]:

print("값의 범위 : {} ~ {}".format(img_array.min(), img_array.max()))

Out [16]:

값의 범위 : 0.0 ~ 1.0

In [17]:

# img 변화 확인
plt.imshow(img_array)
plt.show()

Out [17]:

In [18]:

img_array.dtype

Out [18]:

dtype('float64')

In [19]:

# 각 color channel을 별도의 array에 할당
red_array = img_array[:, :, 0]
green_array = img_array[:, :, 1]
blue_array = img_array[:, :, 2]

Axis에 작업

Numpy의 선형 대수 모듈인 numpy.linalg 를 사용하여 이 자습서의 작업을 수행한다. 이 모듈에 있는 대부분의 선형 대수 함수는 scipy.linalg 에서도 찾을 수 있으며 사용자는 실제 응용 프로그램에 scipy 모듈을 사용하는 것이 좋다. 그러나 SVD 함수와 같은 scipy.linalg 모듈의 일부 함수는 2D 배열만 지원한다.

SVD (Singular Value Decomposition) 특이값 분해

특잇값 분해는 행렬을 특정한 구조로 분해하는 방식으로, 신호 처리와 통계학 등의 분야에서 자주 사용된다.

\[M=U\Sigma V^{*}\!\]

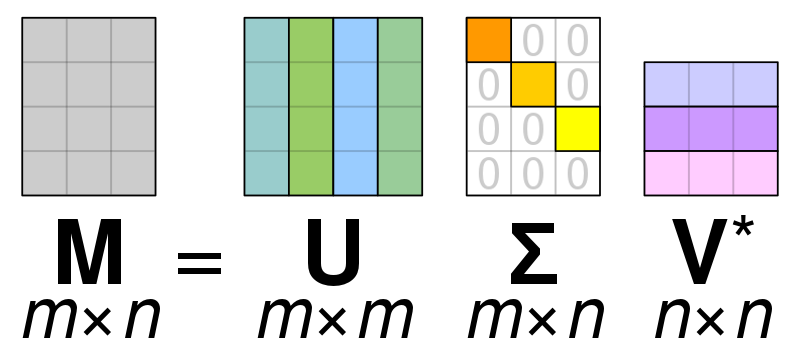
M (768x1024) =
U 전치행렬(768x768)
sigma 대각으로만 값 나머지 0(768,)
V^* 전치행렬(1024x1024)

모두 곱하면 원래값이 복원된다

In [20]:

# 선형대수 하위 모듈 불러오기
from numpy import linalg

\[U \Sigma V^T = A\]

rgb로 작업 시 복잡해지므로 grayscale로 바꿔서 작업(채널을 하나로 합침)

\[Y = 0.2126 R + 0.7152 G + 0.0722 B\]

array 곱셈 연산자 @를 사용

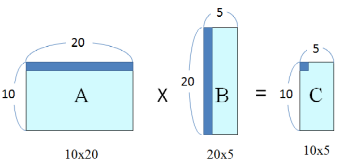
행렬곱의 전제조건: 앞쪽의 열과 뒤쪽의 행이 같아야 함
행렬곱의 결과: 앞쪽 array 행 x 뒤쪽 array 열

각 위치값들을 곱해서 더한다

In [21]:

img_gray = img_array @ [0.2126, 0.7152, 0.0722]
# (768, 1024, 3) @ (3, ) = (768, 1024)

In [22]:

img_gray.shape

Out [22]:

(768, 1024)

In [23]:

plt.imshow(img_gray, cmap="gray") # 그냥 하면 임의 색으로 정해지므로 colormap지정
plt.show()

Out [23]:

특이값 분해

In [24]:

# 특이값 분해
U, s, Vt = linalg.svd(img_gray)

In [25]:

U.shape, s.shape, Vt.shape

Out [25]:

((768, 768), (768,), (1024, 1024))

In [26]:

# 행렬곱을 통해 원래대로 돌아오는지 확인
# 대각행렬의 shape를 조정해줘야 한다
import numpy as np

Sigma = np.zeros((U.shape[1], Vt.shape[0])) # fill_diagonal는 값을 채워주기만 하므로 초기화를 해 줘야 함 # (768, 1024)
np.fill_diagonal(Sigma, s) # 대각선으로 값을 채우기

In [27]:

Sigma[0:2]

Out [27]:

array([[410.42098224,   0.        ,   0.        , ...,   0.        ,
          0.        ,   0.        ],
       [  0.        ,  85.56090199,   0.        , ...,   0.        ,
          0.        ,   0.        ]])

In [28]:

# 데이터 복원
(U @ Sigma @ Vt)[:2]

Out [28]:

array([[0.45209882, 0.51876549, 0.57815529, ..., 0.47355843, 0.51387529,
        0.54524784],
       [0.33250118, 0.41485412, 0.49104706, ..., 0.46907059, 0.53181569,
        0.57887451]])

근사치

In [29]:

linalg.norm(img_gray - U @ Sigma @ Vt) # 8가지 다른 매트릭스 노름 중 1가지를 반환 (벡터값들 사이의 차이값을 구하는 함수)
# 작을수록 근사치(거의 0에 근접: 원상복구 됨)

Out [29]:

1.4108253216554015e-12

In [30]:

np.allclose(img_gray, U @ Sigma @ Vt) # 원래값과 차이가 없다면 True반환

Out [30]:

True

In [31]:

plt.plot(s)
plt.show()

Out [31]:

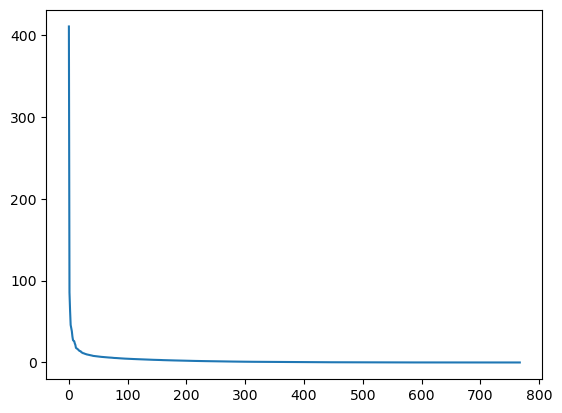
s(sigma)의 대부분의 값이 매우 작음

In [32]:

k = 50 # 임의의 값
approx = U @ Sigma[:, :k] @ Vt[:k, :] # Sigma의 768개 행에 1024열중 10개만 사용, Vt의 1024열중 10개에 1024개 열 사용

In [33]:

plt.imshow(approx, cmap="gray")
plt.show()

Out [33]:

분해해서 합칠 때 모든 정보가 필요한 것이 아니다! 일부만 있어도 가능

Color 이미지에 시도

r, g, b각각에 대해 위의 작업을 해도 되지만 numpy의 broadcast를 활용하면 쉽게 작업할 수 있다.

In [34]:

from PIL import Image

In [35]:

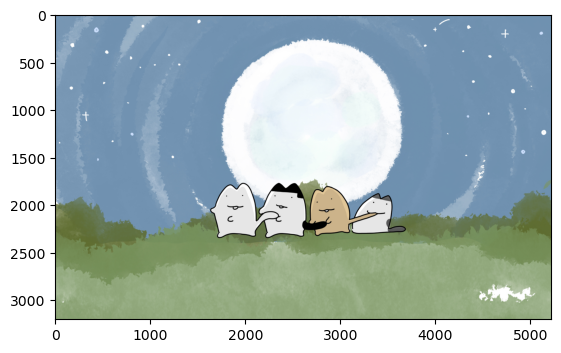
img_path = 'img01.jpg'

In [36]:

img = Image.open(img_path) # .convert('L') : grayscale로 불러옴
plt.imshow(img)
plt.show()

Out [36]:

In [37]:

type(img)

Out [37]:

PIL.JpegImagePlugin.JpegImageFile

In [38]:

# img를 ndarray로 변환
np.array(img)[:2]

Out [38]:

array([[[120, 151, 180],
        [120, 151, 180],
        [120, 151, 180],
        ...,
        [116, 149, 180],
        [117, 150, 181],
        [117, 150, 181]],

       [[120, 151, 180],
        [120, 151, 180],
        [120, 151, 180],
        ...,
        [114, 147, 178],
        [115, 148, 179],
        [116, 149, 180]]], dtype=uint8)

In [39]:

img2 = Image.open(img_path).convert('L')
plt.imshow(img2)
plt.show()

Out [39]:

In [40]:

np.array(img2)[:2]

Out [40]:

array([[145, 145, 145, ..., 143, 144, 144],
       [145, 145, 145, ..., 141, 142, 143]], dtype=uint8)

In [41]:

# opencv 불러오기
import cv2

In [42]:

img3 = cv2.imread(img_path)
img3 = cv2.cvtColor(img3, cv2.COLOR_BGR2RGB) # opencv는 BGR로 불러오기에 RGB로 변환

In [43]:

img3[:2]

Out [43]:

array([[[120, 151, 180],
        [120, 151, 180],
        [120, 151, 180],
        ...,
        [116, 149, 180],
        [117, 150, 181],
        [117, 150, 181]],

       [[120, 151, 180],
        [120, 151, 180],
        [120, 151, 180],
        ...,
        [114, 147, 178],
        [115, 148, 179],
        [116, 149, 180]]], dtype=uint8)

In [44]:

plt.imshow(img3)
plt.show()

Out [44]:

SVD를 적용할 array가 2차원 이상일 경우 모든 axis에 한번에 적용할 수 있다. 하지만 numpy의 선형 대수 함수는 (n, M, N) 형식의 array에 적용해야 한다. 이 형식의 첫번째 axis인 n은 M×N metrix가 얼마나 쌓여 있는지를 나타내는 숫자여야 한다.

In [45]:

img3.shape

Out [45]:

(3200, 5220, 3)

In [46]:

img3_array = img3 / 255

In [47]:

img_array_transposed = np.transpose(img3_array, (2, 0, 1))
img_array_transposed.shape

Out [47]:

(3, 3200, 5220)

In [48]:

# SVD 적용
U, s, Vt = linalg.svd(img_array_transposed)

In [49]:

U.shape, s.shape, Vt.shape

Out [49]:

((3, 3200, 3200), (3, 3200), (3, 5220, 5220))

n차원 array 결과물

In [50]:

# s array가 곱셈이 가능한 형태로 변환
Sigma = np.zeros((3, 3200, 5220))
for j in range(3):
    np.fill_diagonal(Sigma[j, :, :], s[j, :])

In [51]:

Sigma.shape

Out [51]:

(3, 3200, 5220)

In [52]:

# 데이터 복원
reconstructed = U @ Sigma @ Vt

In [53]:

reconstructed.shape

Out [53]:

(3, 3200, 5220)

In [54]:

reconstructed.min(), reconstructed.max()

Out [54]:

(-1.4564213143873975e-14, 1.000000000000282)

In [55]:

img3_array.min(), img3_array.max()

Out [55]:

(0.0, 1.0)

부동 소수점 오류가 누적되면 원본 이미지 범위를 약간 벗어난 값이 생성될 수 있다

In [56]:

# 부동 소수점 오류 제거
reconstructed = np.clip(reconstructed, 0, 1)
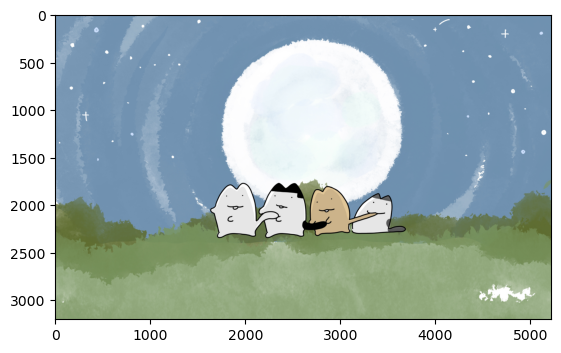
plt.imshow(np.transpose(reconstructed, (1, 2, 0)))
plt.show()

Out [56]:

In [57]:

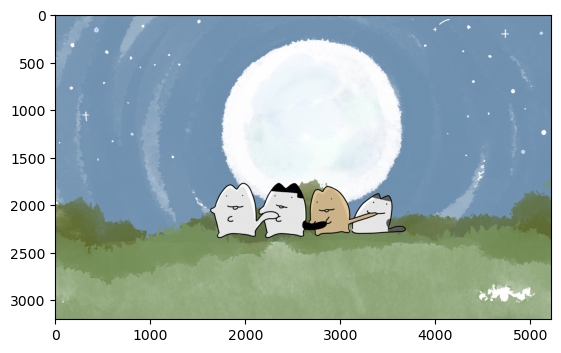
# 근사치(approximation) 수행
k = 50
approx_img = U @ Sigma[..., :k] @ Vt[..., :k, :] # ...은 생략을 의미한다

In [58]:

approx_img.shape

Out [58]:

(3, 3200, 5220)

In [59]:

approx_img = np.clip(approx_img, 0, 1)
plt.imshow(np.transpose(approx_img, (1, 2, 0)))
plt.show()

Out [59]:

Reference

이 포스트는 SeSAC 인공지능 자연어처리, 컴퓨터비전 기술을 활용한 응용 SW 개발자 양성 과정 - 심선조 강사님의 강의를 정리한 내용입니다.
NumPy.org : NumPy
Wikipedia : 특잇값 분해
Seo Young Ki : [Algorithm] 연속 행렬 곱셈 (동적계획)
정은규 주간야옹이 배경화면

Twitter Facebook LinkedIn

Kwak Jisub

Numpy (2)

N차원 배열의 선형 대수학

데이터 shape, axis, array 정보

Axis에 작업

특이값 분해

근사치

Color 이미지에 시도

n차원 array 결과물

Reference

공유하기

댓글남기기

참고

python max 함수의 매개변수

python round 함수의 문제

python set 자료형과 메소드

MySQL GROUP BY와 MAX