Python (7) - Numpy

2022년 11월 10일 11 분 소요

What is Numpy?

numpy는 “numerical python”의 약자

Numerical Computing : 컴퓨터가 실수값을 효과적으로 계산할 수 있도록 하는 연구 분야. Vector Arithmetic : 벡터 연산 –> 데이터가 벡터로 표현되기 때문이다.
numpy는 다양한 머신러닝 라이브러리들에 의존성을 가지고 있고, 일반 파이썬 리스트에 비해 강력한 성능을 자랑한다.

성능 : numpy array » python list(or tuple)
python list와 비슷한 개념을 numpy에서는 numpy array라고 부른다.

파이썬 리스트처럼 여러 데이터를 한번에 다룰 수 있으나, 모든 데이터가 동일한 data type을 가져야한다.
C언어와 JAVA에서 사용하는 array와 비슷한 개념이며, 동적 할당(dynamic type binding)을 지원하는 파이썬의 리스트와 구조가 다르다.

Numpy의 특징

자료형 통일

numpy array는 모든 원소의 자료형이 동일해야 한다.
(아래는 numpy array가 지원하는 data types)

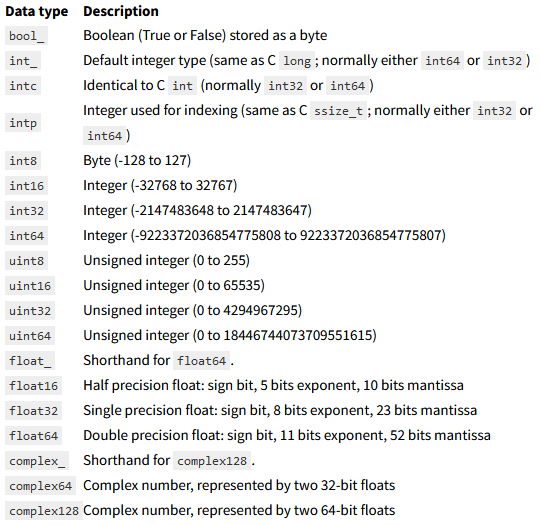
더 자세한 지원 data type은 Numpy Documentation에서 확인가능하다.

선언 후 변경불가

numpy array는 선언할 때 크기를 지정한 뒤, 변경할 수 없다. list.append(), pop()을 통해 자유롭게 원소 변경 및 크기 변경이 가능하지만, numpy array는 만들어지고 나면 원소의 update는 가능하지만, array의 크기를 변경할 수는 없다.

numpy의 경우에는 append라는 함수가 있으나, 의미가 다릅니다.

numpy array의 크기를 변경하는 경우에는 복사가 일어난다.

C, C++로 구현됨

사실 numpy array는 C, C++로 구현이 되어 있다. 이는 high performance를 내기 위해서이며, python이 Numerical computing에 취약하다는 단점을 보완한다.

type checking pass

numpy array가 python list보다 빠른 이유 중에 하나는 C, C++에서 처럼 원소의 타입을 지정하여 원소의 type checking을 할 필요가 없기 때문이다.

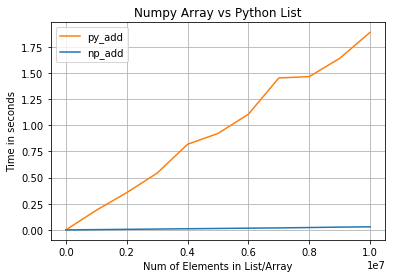
아래의 그래프는 두 array/list에서 랜덤으로 두개를 뽑아 서로 더할 때 array/list의 원소 수에 따른 걸리는 시간을 나타낸 것이다. 자세한 코드는 여기에서 확인 할 수 있다.

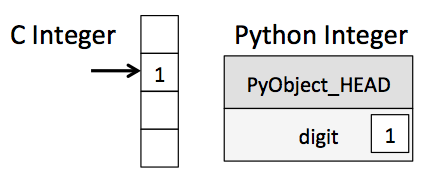
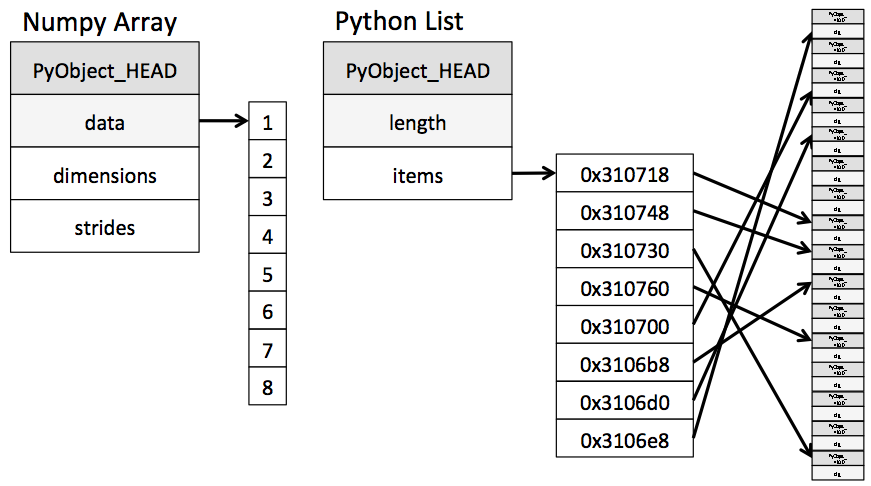
(python list와 numpy array의 내부 구현 비교)

같은 연산에 대한 속도

numpy array는 universal function(through broadcast)을 제공하기 때문에 같은 연산 반복에 대해 훨씬 빠르다. 데이터의 크기가 클수록 차이가 더 크다.

아래는 big_array라는 1000000개의 원소를 가지는 array를 만든 뒤에 for문을 돌면서 각 원소를 뒤집는 연산을 했을 때의 걸리는 시간과, numpy array에 있는 UFuncs(Universal function)을 사용했을 때 걸리는 시간을 측정한 것이다.
거의 1000배정도 차이가 나는 것을 볼 수 있다.

In [1]:

import numpy as np
np.random.seed(0)

def compute_reciprocals(values):
    output = np.empty(len(values))
    for i in range(len(values)):
        output[i] = 1.0 / values[i]
    return output

In [2]:

big_array = np.random.randint(1, 100, size=1000000)

%timeit compute_reciprocals(big_array) # for문 연산
%timeit (1.0 / big_array) # UFuncs 사용

Out [2]:

2.57 s ± 16.9 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
5.86 ms ± 626 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

Numpy Basics

numpy의 기본적인 사용법에 대해서 배워보자.
numpy에서 numpy.array를 만드는 여러가지 방법과 지원하는 연산자에 대해서

Numpy array Creation

In [3]:

# numpy 라이브러리를 불러오기
import numpy as np

In [4]:

# 파이썬 리스트 선언
data = [1, 2, 3, 4, 5]
data, type(data)

Out [4]:

([1, 2, 3, 4, 5], list)

In [5]:

# 파이썬 2차원 리스트(행렬) 선언
data2 = [
        [1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]
        ]
data2

Out [5]:

[[1, 2, 3], [4, 5, 6], [7, 8, 9]]

In [6]:

# 파이썬 list를 numpy array로 변환
arr1 = np.array(data)
print(arr1)  # 콤마가 사라져 보여진다!
arr1, type(arr1)  # numpy.ndarray : ndarray(n-dimensional array)
# numpy array를 만드는 방식의 대부분은 파이썬 리스트를 np.array로 변환하는 방식
# np.array([1,2,3,4,5])
# np.array((1,2,3,4,5))
arr1.shape  # np.array.shape는 np.array의 크기 // 5×1 = (5,)

Out [6]:

[1 2 3 4 5]

(5,)

In [7]:

# 2차원 리스트를 np.array로 만들기
arr2 = np.array(data2)
print(arr2)
print(type(arr2))
arr2.shape

Out [7]:

[[1 2 3]
 [4 5 6]
 [7 8 9]]
<class 'numpy.ndarray'>

(3, 3)

numpy 기본 함수들

In [8]:

print("arr2의 ndim : ", arr2.ndim)  # arr2의 차원
print("arr2의 shape : ", arr2.shape)  # arr2의 행, 열 크기
print("arr2의 size : ", arr2.size)  # arr2의 행 × 열
print("arr2의 dtype : ", arr2.dtype)  # arr2의 원소 타입. # int64: integer + 64bits
print("arr2의 itemsize : ", arr2.itemsize)  # arr2의 원소 사이즈(bytes) # 64bits = 8B
# itemsize * size # numpy array가 차지하는 메모리 공간
print("arr2의 nbytes : ", arr2.nbytes)

Out [8]:

arr2의 ndim :  2
arr2의 shape :  (3, 3)
arr2의 size :  9
arr2의 dtype :  int32
arr2의 itemsize :  4
arr2의 nbytes :  36

Array Initialization

numpy array를 초기값과 함께 생성하는 방법도 있다.
원소가 0인 array를 생성하는 np.zeros()
원소가 1인 array를 생성하는 np.ones()
특정 범위의 원소를 가지는 np.arange()

In [9]:

# 0이 5개 있는 array
np.zeros(5)

Out [9]:

array([0., 0., 0., 0., 0.])

In [10]:

# 0이 3x3인 array
np.zeros((3, 3))

Out [10]:

array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]])

In [11]:

# 1이 3개 있는 array
np.ones(3)

Out [11]:

array([1., 1., 1.])

In [12]:

# 1이 2x2인 array
np.ones((2, 2))

Out [12]:

array([[1., 1.],
       [1., 1.]])

In [13]:

# 0부터 9까지 숫자를 자동으로 생성한 array
np.arange(10)

Out [13]:

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [14]:

# 10부터 99까지 숫자를 자동으로 생성한 array
np.arange(10, 100)  # python range 함수와 동일한데, np.array 생성까지 자동으로

Out [14]:

array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26,
       27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43,
       44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
       61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77,
       78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94,
       95, 96, 97, 98, 99])

Array Operation (like vector) –> Universal Function

numpy array를 쓰는 가장 큰 이유는 vector처럼 사용할 수 있기 때문이다.

e.g. arr1 = np.array([1, 2, 3, 4, 5]) –> (1, 2, 3, 4, 5) # vector
그렇기 때문에 scipy, matplotlib, scikit-learn, pandas, tensorflow, pytorch 등 대부분의 데이터분석 라이브러리들이 numpy array를 사용한다.

대부분의 데이터 분석 라이브러리들은 벡터를 사용하는데, 그 벡터가 바로 numpy array로 표현되기 때문이다.
데이터 분석은 99.9% 데이터를 벡터로 표현하여 분석하기 때문에, 이 특징은 굉장히 중요하다.

벡터 == numpy array
두 벡터 A = (1, 2), B = (2, 1)이라고 할 때, 벡터의 연산은 다음과 같이 정의된다.

A + B = (3, 3)

A - B = (-1, 1)

A o B = 1x2 + 2x1 = 4 (dot product)

In [15]:

v1 = np.array((1, 2, 3))
v2 = np.array((4, 5, 6))
type(v1), type(v2)

Out [15]:

(numpy.ndarray, numpy.ndarray)

In [16]:

# 리스트로 더하기 연산해보기
t1 = (1, 2, 3)
t2 = (4, 5)
#type(t1), type(t2)
t1 + t2

Out [16]:

(1, 2, 3, 4, 5)

In [17]:

# vector addition
v1 + v2

Out [17]:

array([5, 7, 9])

In [18]:

# vector substraction
v1 - v2

Out [18]:

array([-3, -3, -3])

In [19]:

# (not vector operation) elementwise multiplication
v1 * v2

Out [19]:

array([ 4, 10, 18])

In [20]:

# (not vector operation) elementwise division
v1 / v2

Out [20]:

array([0.25, 0.4 , 0.5 ])

In [21]:

# dot product
v1 @ v2  # 1x4 + 2x5 + 3x6 = 32

Out [21]:

Broadcast

서로 크기가 다른 numpy array를 연산할 때, 자동으로 연산을 전파(broadcast)해주는 기능. 행렬곱 연산을 할 때 편리하다.

In [22]:

arr1 = np.array([[1, 2, 3],
                [4, 5, 6]])
arr1.shape

Out [22]:

(2, 3)

In [23]:

arr2 = np.array([7, 8, 9])
arr2.shape

Out [23]:

(3,)

In [24]:

arr1 + arr2 # [1, 2, 3] + [7, 8, 9] // [4, 5, 6] + [7, 8, 9]

Out [24]:

array([[ 8, 10, 12],
       [11, 13, 15]])

In [25]:

print(arr1)
print(arr2)
arr1 * arr2 # [1, 2, 3] * [7, 8, 9] // [4, 5, 6] * [7, 8, 9]

Out [25]:

[[1 2 3]
 [4 5 6]]
[7 8 9]

array([[ 7, 16, 27],
       [28, 40, 54]])

In [26]:

arr1 * 10  # vector scalar multiplication

Out [26]:

array([[10, 20, 30],
       [40, 50, 60]])

In [27]:

arr1 * arr1

Out [27]:

array([[ 1,  4,  9],
       [16, 25, 36]])

Universal Functions

numpy array는 하나의 함수를 모든 원소에 자동으로 적용해주는 Universal Function이라는 기능을 제공한다. 이 덕분에 모든 원소에 대해 같은 작업을 처리할 때 엄청나게 빠른 속도를 낼 수 있다.

In [28]:

arr1 = np.array([1, 2, 3])
arr1 = arr1 / 1
arr1.dtype

Out [28]:

dtype('float64')

In [29]:

# 모든 원소를 역수 취하기
1 / arr1  # 각 원소에 1 / 라는 operation을 모두 적용

Out [29]:

array([1.        , 0.5       , 0.33333333])

In [30]:

# 모든 원소에 2더하기
arr1 + 2

Out [30]:

array([3., 4., 5.])

Indexing (same as python list, but more powerful)

In [31]:

arr1 = np.arange(10)
arr1

Out [31]:

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [32]:

# 첫번째 원소
arr1[0]

Out [32]:

In [33]:

# 마지막 원소
arr1[-1]

Out [33]:

In [34]:

# 앞에서부터 원소 3개 slicing
arr1[:3]

Out [34]:

array([0, 1, 2])

In [35]:

arr2 = np.array([[1, 2, 3, 4, ],
                 [5, 6, 7, 8],
                 [9, 10, 11, 12]])
arr2

Out [35]:

array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

In [36]:

# arr2의 2, 3 원소 = 7
arr2[1, 2]

Out [36]:

In [37]:

# arr2의 세번째 columnm (3, 7, 11)
arr2[:, 2] # arr2에 있는 모든 row에 대해서 3번째 원소를 indexing --> numpy array
# arr2[0, 2]
# arr2[1, 2]
# arr2[2, 2]

Out [37]:

array([ 3,  7, 11])

In [38]:

# arr2의 두번째 row
#arr2[1]
arr2[1, :] # arr2에 있는 두번째 row에 대해서 모든 원소를 indexing --> numpy array

Out [38]:

array([5, 6, 7, 8])

Masking

In [39]:

mask = np.array([1, 0, 0, 1, 1, 0, 0])
mask

Out [39]:

array([1, 0, 0, 1, 1, 0, 0])

In [40]:

data = np.random.randn(7, 4)
data

Out [40]:

array([[ 1.51902497,  0.75597591, -1.5697609 , -0.44150337],
       [-0.66162637, -0.74112867,  1.54345144, -1.49533138],
       [-0.38729976,  0.90898697, -0.80846432, -1.55328005],
       [ 1.09581535,  1.0034082 , -0.96307811,  0.38494418],
       [-2.10187333,  0.43009583, -0.66377698, -0.76175201],
       [-0.26793866,  1.50540723,  1.04358096, -0.08576194],
       [-1.87303454, -1.32328083,  1.18421646,  0.20064575]])

In [41]:

data.shape

Out [41]:

(7, 4)

In [42]:

# mask 만들기
masked_data = (mask == 1)
masked_data

Out [42]:

array([ True, False, False,  True,  True, False, False])

In [43]:

# data에 mask 적용
data[masked_data, :]

Out [43]:

array([[ 1.51902497,  0.75597591, -1.5697609 , -0.44150337],
       [ 1.09581535,  1.0034082 , -0.96307811,  0.38494418],
       [-2.10187333,  0.43009583, -0.66377698, -0.76175201]])

In [44]:

# mask 바로 지정
data[mask == 0, :]

Out [44]:

array([[-0.66162637, -0.74112867,  1.54345144, -1.49533138],
       [-0.38729976,  0.90898697, -0.80846432, -1.55328005],
       [-0.26793866,  1.50540723,  1.04358096, -0.08576194],
       [-1.87303454, -1.32328083,  1.18421646,  0.20064575]])

In [45]:

# fancy indexing을 이용해서 masking
data[:, 0] < 0 # 7 x 1의 mask == 첫번째 column의 원소중에 0보다 작은 원소들의 위치가 True.

Out [45]:

array([False,  True,  True, False,  True,  True,  True])

In [46]:

# fancy indexing의 또 다른 방법
data[data[:, 0] < 0, 0]

Out [46]:

array([-0.66162637, -0.38729976, -2.10187333, -0.26793866, -1.87303454])

In [47]:

data < 0

Out [47]:

array([[False, False,  True,  True],
       [ True,  True, False,  True],
       [ True, False,  True,  True],
       [False, False,  True, False],
       [ True, False,  True,  True],
       [ True, False, False,  True],
       [ True,  True, False, False]])

In [48]:

data[data < 0] = 0 # 2차원 data에서 첫번째 column에 0보다 작은 원소들을 0으로 치환
data

Out [48]:

array([[1.51902497, 0.75597591, 0.        , 0.        ],
       [0.        , 0.        , 1.54345144, 0.        ],
       [0.        , 0.90898697, 0.        , 0.        ],
       [1.09581535, 1.0034082 , 0.        , 0.38494418],
       [0.        , 0.43009583, 0.        , 0.        ],
       [0.        , 1.50540723, 1.04358096, 0.        ],
       [0.        , 0.        , 1.18421646, 0.20064575]])

Numpy Methods

In [49]:

# 표준정규분포에서 random sampling을 한 원소를 가지는 5x3 행렬을 만든다.
import numpy as np
mat1 = np.random.randn(5, 3)
mat1

Out [49]:

array([[ 1.1674455 ,  1.54779839,  0.34931167],
       [-0.32194254,  0.4458342 , -0.02987065],
       [-1.61419773,  0.88510108,  0.56279957],
       [ 0.16638679,  0.93883187, -0.33503193],
       [ 1.92448314, -0.52839303, -0.51714191]])

In [50]:

# mat1에 절대값 씌우기
np.abs(mat1)

Out [50]:

array([[1.1674455 , 1.54779839, 0.34931167],
       [0.32194254, 0.4458342 , 0.02987065],
       [1.61419773, 0.88510108, 0.56279957],
       [0.16638679, 0.93883187, 0.33503193],
       [1.92448314, 0.52839303, 0.51714191]])

In [51]:

# mat1의 square root(제곱근) 구하기
comp1 = np.array(mat1, dtype=complex)
print(np.sqrt(comp1))
# imagnary numbers = nan

Out [51]:

[[1.08048392+0.j         1.24410546+0.j         0.59102595+0.j        ]
 [0.        +0.56739981j 0.66770817+0.j         0.        +0.17283128j]
 [0.        +1.27051081j 0.94079811+0.j         0.75019969+0.j        ]
 [0.40790537+0.j         0.96893337+0.j         0.        +0.57881942j]
 [1.38725742+0.j         0.        +0.72690648j 0.        +0.71912579j]]

In [52]:

# mat1 제곱하기
np.square(mat1)

Out [52]:

array([[1.36292900e+00, 2.39567985e+00, 1.22018646e-01],
       [1.03647002e-01, 1.98768130e-01, 8.92255753e-04],
       [2.60563431e+00, 7.83403925e-01, 3.16743356e-01],
       [2.76845649e-02, 8.81405272e-01, 1.12246391e-01],
       [3.70363535e+00, 2.79199195e-01, 2.67435751e-01]])

In [53]:

# mat1의 지수값 구하기
np.exp(mat1)

Out [53]:

array([[3.21377257, 4.70110877, 1.4180911 ],
       [0.72473983, 1.56179249, 0.97057107],
       [0.1990503 , 2.42322932, 1.7555805 ],
       [1.18102983, 2.55699276, 0.71531525],
       [6.85160643, 0.5895516 , 0.59622217]])

In [54]:

# mat1의 log값(자연로그) 구하기
np.log(mat1)
# log의 밑이 음수가 될 수 없다.(자연로그)

Out [54]:

C:\Users\user\AppData\Local\Temp\ipykernel_17020\302438178.py:2: RuntimeWarning: invalid value encountered in log
  np.log(mat1)

array([[ 0.15481803,  0.43683353, -1.0517907 ],
       [        nan, -0.80780815,         nan],
       [        nan, -0.12205342, -0.57483172],
       [-1.79344012, -0.06311887,         nan],
       [ 0.65465743,         nan,         nan]])

In [55]:

# 상용로그
np.log10(mat1)

Out [55]:

C:\Users\user\AppData\Local\Temp\ipykernel_17020\786002492.py:2: RuntimeWarning: invalid value encountered in log10
  np.log10(mat1)

array([[ 0.06723662,  0.18971439, -0.4567869 ],
       [        nan, -0.35082662,         nan],
       [        nan, -0.05300713, -0.24964624],
       [-0.77888115, -0.02741218,         nan],
       [ 0.28431411,         nan,         nan]])

In [56]:

# 이진로그
np.log2(mat1)

Out [56]:

C:\Users\user\AppData\Local\Temp\ipykernel_17020\3364023338.py:2: RuntimeWarning: invalid value encountered in log2
  np.log2(mat1)

array([[ 0.22335521,  0.63021756, -1.51741323],
       [        nan, -1.16542082,         nan],
       [        nan, -0.17608587, -0.82930687],
       [-2.58738717, -0.09106128,         nan],
       [ 0.94447103,         nan,         nan]])

In [57]:

# 부호찾기
np.sign(mat1)

Out [57]:

array([[ 1.,  1.,  1.],
       [-1.,  1., -1.],
       [-1.,  1.,  1.],
       [ 1.,  1., -1.],
       [ 1., -1., -1.]])

In [58]:

# 올림
np.ceil(mat1)

Out [58]:

array([[ 2.,  2.,  1.],
       [-0.,  1., -0.],
       [-1.,  1.,  1.],
       [ 1.,  1., -0.],
       [ 2., -0., -0.]])

In [59]:

# 내림
np.floor(mat1)

Out [59]:

array([[ 1.,  1.,  0.],
       [-1.,  0., -1.],
       [-2.,  0.,  0.],
       [ 0.,  0., -1.],
       [ 1., -1., -1.]])

In [60]:

# 존배하지 않는 값이 있는지 없는지 # nan = not a number
np.isnan(mat1)

Out [60]:

array([[False, False, False],
       [False, False, False],
       [False, False, False],
       [False, False, False],
       [False, False, False]])

In [61]:

# 함수안의 함수
np.isnan(np.log(mat1))

Out [61]:

C:\Users\user\AppData\Local\Temp\ipykernel_17020\755047098.py:2: RuntimeWarning: invalid value encountered in log
  np.isnan(np.log(mat1))

array([[False, False, False],
       [ True, False,  True],
       [ True, False, False],
       [False, False,  True],
       [False,  True,  True]])

In [62]:

# 무한(infinite)인지 확인
np.isinf(mat1)

Out [62]:

array([[False, False, False],
       [False, False, False],
       [False, False, False],
       [False, False, False],
       [False, False, False]])

In [63]:

np.sin(mat1)

Out [63]:

array([[ 0.91975095,  0.99973556,  0.34225113],
       [-0.3164099 ,  0.43121068, -0.02986621],
       [-0.99905831,  0.773979  ,  0.53355606],
       [ 0.16562013,  0.8068686 , -0.32879932],
       [ 0.93810213, -0.50414618, -0.4943978 ]])

In [64]:

np.cos(mat1)

Out [64]:

array([[ 0.39250246,  0.02299591,  0.93960852],
       [ 0.94862257,  0.90225127,  0.99955391],
       [-0.04338778,  0.63321127,  0.8457647 ],
       [ 0.98618962,  0.59073096,  0.94439981],
       [-0.34635876,  0.86361833,  0.86923576]])

In [65]:

np.tan(mat1)

Out [65]:

array([[ 2.34329983e+00,  4.34744923e+01,  3.64248649e-01],
       [-3.33546669e-01,  4.77927492e-01, -2.98795376e-02],
       [ 2.30262616e+01,  1.22230768e+00,  6.30856387e-01],
       [ 1.67939438e-01,  1.36588169e+00, -3.48156910e-01],
       [-2.70846948e+00, -5.83760402e-01, -5.68772966e-01]])

In [66]:

np.tanh(mat1)

Out [66]:

array([[ 0.82345154,  0.9134215 ,  0.33576496],
       [-0.31126232,  0.4184687 , -0.02986177],
       [-0.92377795,  0.70896562,  0.51005164],
       [ 0.16486816,  0.73468509, -0.32303491],
       [ 0.95828511, -0.48415176, -0.47549112]])

In [67]:

mat2 = np.random.randn(5, 3)
mat2

Out [67]:

array([[ 0.58984159,  0.6874401 , -0.76382639],
       [ 0.02296139,  1.14834405,  0.28572605],
       [-0.79750452, -0.70672748,  0.91207449],
       [-0.7533038 , -1.57031679, -0.4134728 ],
       [-1.39769075,  0.91228177,  0.56870329]])

In [68]:

# 비교
np.maximum(mat1, mat2)

Out [68]:

array([[ 1.1674455 ,  1.54779839,  0.34931167],
       [ 0.02296139,  1.14834405,  0.28572605],
       [-0.79750452,  0.88510108,  0.91207449],
       [ 0.16638679,  0.93883187, -0.33503193],
       [ 1.92448314,  0.91228177,  0.56870329]])

Reshaping array

In [69]:

x = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9]])
x

Out [69]:

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

In [70]:

# x를 3x3 행렬로 변형
x1 = np.arange(1, 10).reshape(3, 3)
x1

Out [70]:

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

In [71]:

# 비교
x == x1

Out [71]:

array([[ True,  True,  True],
       [ True,  True,  True],
       [ True,  True,  True]])

In [72]:

# (1,2,3)을 transpose
x2 = np.array([1, 2, 3]).reshape(3, 1)  # row vector -> column vecor
x2

Out [72]:

array([[1],
       [2],
       [3]])

Concatenation of arrays

In [73]:

arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
# arr1와 arr2를 합치기
# arr1 + arr2?
np.concatenate([arr1, arr2])
#arr1 + arr2 # array([1, 2, 3, 4, 5, 6])

Out [73]:

array([1, 2, 3, 4, 5, 6])

In [74]:

# stacking vertically
np.vstack([arr1, arr2])

Out [74]:

array([[1, 2, 3],
       [4, 5, 6]])

In [75]:

# stacking horizontally
np.hstack([arr1, arr2])

Out [75]:

array([1, 2, 3, 4, 5, 6])

Aggregation functions

In [76]:

mat1

Out [76]:

array([[ 1.1674455 ,  1.54779839,  0.34931167],
       [-0.32194254,  0.4458342 , -0.02987065],
       [-1.61419773,  0.88510108,  0.56279957],
       [ 0.16638679,  0.93883187, -0.33503193],
       [ 1.92448314, -0.52839303, -0.51714191]])

In [77]:

np.sum(mat1) # 15개 숫자의 총합.

Out [77]:

4.641414427263748

In [78]:

# 다른 축으로 더해보기
np.sum(mat1, axis=0) # column별 총합.

Out [78]:

array([1.32217516, 3.2891725 , 0.03006676])

In [79]:

# 평균
np.mean(mat1)

Out [79]:

0.3094276284842499

In [80]:

mat3 = np.random.rand(5, 3)
mat3

Out [80]:

array([[0.72199978, 0.28087945, 0.0323053 ],
       [0.10372152, 0.53005891, 0.69079487],
       [0.99206462, 0.19107554, 0.80362599],
       [0.27757786, 0.95501989, 0.34106202],
       [0.05331828, 0.90524432, 0.82573516]])

In [81]:

np.mean(mat3)

Out [81]:

0.5136322344117528

In [82]:

np.mean(mat3, axis=0)

Out [82]:

array([0.42973641, 0.57245562, 0.53870467])

In [83]:

np.mean(mat3, axis=1)

Out [83]:

array([0.34506151, 0.4415251 , 0.66225538, 0.52455326, 0.59476592])

In [84]:

np.std(mat3) # 표준편차

Out [84]:

0.33555614526975874

In [85]:

np.min(mat3, axis=0)

Out [85]:

array([0.05331828, 0.19107554, 0.0323053 ])

In [86]:

np.max(mat3, axis=1)

Out [86]:

array([0.72199978, 0.69079487, 0.99206462, 0.95501989, 0.90524432])

In [87]:

# 최소값이 있는 Index
np.argmin(mat3, axis=0)

Out [87]:

array([4, 2, 0], dtype=int64)

In [88]:

# 최대값이 있는 Index
np.argmax(mat3, axis=1)

Out [88]:

array([0, 2, 0, 1, 1], dtype=int64)

In [89]:

np.cumsum(mat3)

Out [89]:

array([0.72199978, 1.00287923, 1.03518454, 1.13890605, 1.66896497,
       2.35975984, 3.35182446, 3.5429    , 4.34652599, 4.62410385,
       5.57912373, 5.92018576, 5.97350404, 6.87874836, 7.70448352])

In [90]:

np.cumsum(mat3, axis=1) # row별 누적합.

Out [90]:

array([[0.72199978, 1.00287923, 1.03518454],
       [0.10372152, 0.63378043, 1.3245753 ],
       [0.99206462, 1.18314016, 1.98676615],
       [0.27757786, 1.23259774, 1.57365977],
       [0.05331828, 0.9585626 , 1.78429776]])

In [91]:

np.cumprod(mat3, axis=0)

Out [91]:

array([[0.72199978, 0.28087945, 0.0323053 ],
       [0.07488691, 0.14888266, 0.02231634],
       [0.07429266, 0.02844783, 0.01793399],
       [0.020622  , 0.02716825, 0.0061166 ],
       [0.00109953, 0.0245939 , 0.00505069]])

In [92]:

# 그냥 정렬
np.sort(mat3)

Out [92]:

array([[0.0323053 , 0.28087945, 0.72199978],
       [0.10372152, 0.53005891, 0.69079487],
       [0.19107554, 0.80362599, 0.99206462],
       [0.27757786, 0.34106202, 0.95501989],
       [0.05331828, 0.82573516, 0.90524432]])

In [93]:

# index를 정렬
np.argsort(mat3, axis=0) # argument sorting에서 정렬된 값의 원래 위치를 보여준다.
# 정렬된 다음의 index를 원래 원소의 위치에 표시해준다.

Out [93]:

array([[4, 2, 0],
       [1, 0, 3],
       [3, 1, 1],
       [0, 4, 2],
       [2, 3, 4]], dtype=int64)

Powerful Numpy

맨 처음에도 봤듯이 numpy는 파이썬 리스트에 비해 연산이 빠르다.
직접 실험을 통해 그 차이를 확인해보자.

In [94]:

np.random.seed(0)

def reverse_num(values):
    output = np.empty(len(values))
    
    for i in range(len(values)):
        output[i] = 1.0 / values[i]
    
    return output

def cum_sum(values):
    total = 0.0
    for num in values:
        total += num
    return total

In [95]:

# 1부터 100까지 범위에서 1000000개를 랜덤으로 뽑아서 array를 만들기
big_array = np.random.randint(1, 100, size=1000000)

In [96]:

%timeit reverse_num(big_array)

Out [96]:

2.67 s ± 58.1 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

In [97]:

%timeit 1.0 / big_array

Out [97]:

5.17 ms ± 133 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

In [98]:

%timeit cum_sum(big_array)

Out [98]:

216 ms ± 1.28 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

In [99]:

%timeit np.sum(big_array)

Out [99]:

368 µs ± 13.8 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

numpy가 파이썬(정확히는 CPython)으로 구현한 함수를 통해 반복문을 수행한것보다 빠른 이유
매번 반복할 때마다 “type matching” 과 “function dispatching” 을 파이썬 interpreter가 수행하기 때문에 “performance bottleneck” 이 생긴다.

In [100]:

# numpy 버전 확인
np.version.version

Out [100]:

'1.23.4'

Reference

이 포스트는 SeSAC 인공지능 SW 개발자 양성 과정 - 나예진 강사님의 강의내용을 정리한 것입니다.
Python Data Science Handbook: Understanding Data Types in Python
Cory Gough: Performance of Numpy Array vs Python List

Twitter Facebook LinkedIn

Kwak Jisub