음성 처리 - 신호처리의 기초(1)

---

신호처리의 기초

• sound: 소리
• acoustics: 음향, hi-fi(오디오)

• speech: 음성(발화, 청취) => 서비스 현장(고객 응대)

• 디지털 신호처리 시스템
  (analog input: 실제 소리;공기의 진동;성대->마이크 수음->전기 진동) -> (analog-digital converter: 사운드 카드)
  -> (digital signal processing: PC 프로그램) -> (digital-analog converter: 사운드 카드)
  -> (analog output: 스피커->변형된 공기 진동)

• 아날로그 신호 처리 시스템(카세트 테이프)
  (analog input: 실제 소리;공기의 진동;성대->마이크 수음->전기 진동)
  -> (analog signal processing: 저항, 콘덴서, 코일, 트랜지스터(진공관), 전기 회로, 카세트 테이프)
  -> (analog output: 스피커->변형된 공기 진동)

ADC(analog digital converter)

In [1]:

import numpy as np
import matplotlib.pyplot as plt

샘플링 레이트(Sampling rate)

아날로그 신호를 초당 몇개의 점으로 표현할 지를 의미한다.
타이밍의 문제

In [2]:

# 아날로그 신호와 디지털 신호
X_analog = np.linspace(0, 2*np.pi, 1000) # 1초 음성 신호라 가정
y_analog = np.sin(X_analog)
X_digital = np.linspace(0, 2*np.pi, 60) # 디지털 샘플링(sampling rate: 60Hz), 초당 몇개의 점으로 표현하는지
                                        # (CD음질: 44100Hz, 옛전화기: 8000Hz, 음성: 16000Hz, 고급장비: 192000Hz)
y_digital = np.sin(X_digital)

plt.plot(X_analog, y_analog)
plt.plot(X_digital, y_digital, 'o')
plt.legend(['analog', 'digital'])
plt.show()

Out [2]:

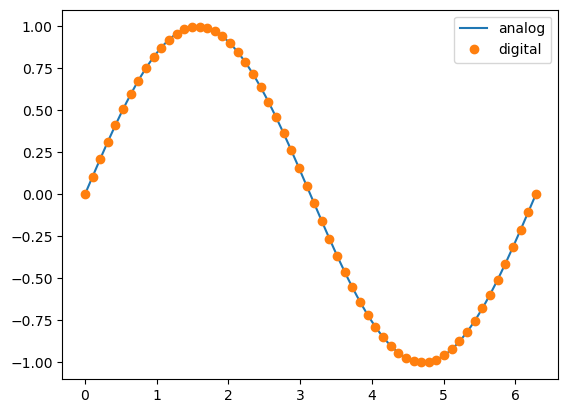
• 아날로그 신호의 특징: 연속적, 자연에 실제하므로 끊기지 않음
• 디지털 신호의 특징: 단계적, 원상 복구를 고려해 빈도를 고려할 필요가 있음

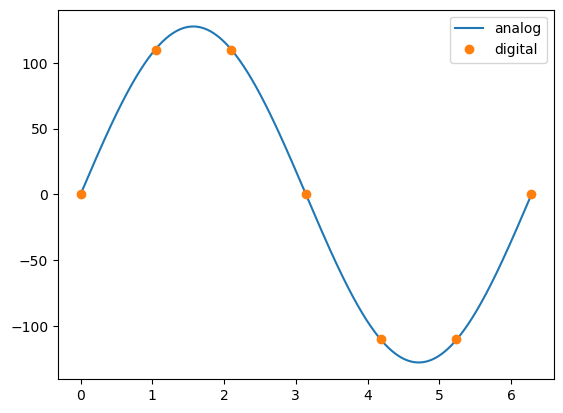
진폭 표현력(bit)

폭, 진폭의 문제

In [3]:

# 아날로그 신호와 디지털 신호
X_analog = np.linspace(0, 2*np.pi, 1000)
y_analog = np.sin(X_analog) * 255.0/2 # 범위를 255로 고정(-127.5~127.5)
X_digital = np.linspace(0, 2*np.pi, 7)
y_digital = (np.sin(X_digital) * 255.0/2).astype(int) # 진폭 표현력(Quantize;양자화) 8bit, 16bit, 24bit

plt.plot(X_analog, y_analog)
plt.plot(X_digital, y_digital, 'o')
plt.legend(['analog', 'digital'])
plt.show()

Out [3]:

In [4]:

# 아날로그 신호와 디지털 신호
X_analog = np.linspace(0, 2*np.pi, 1000)
y_analog = np.sin(X_analog) * 4.0/2
X_digital = np.linspace(0, 2*np.pi, 7)
y_digital = (np.sin(X_digital) * 4.0/2).astype(int) # 4bit

plt.plot(X_analog, y_analog)
plt.plot(X_digital, y_digital, 'o')
plt.legend(['analog', 'digital_quantized'])
plt.show()

Out [4]:

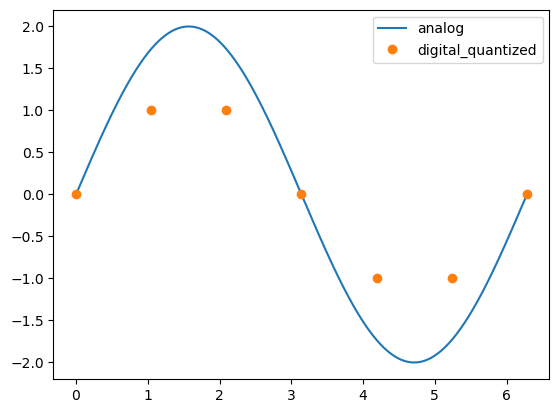
디지털 신호는 정수로 표현하여 0,1로 바꿔서 넣는다.
하지만 아날로그 신호는 sin파를 나타낸다.
표현력(bit수)을 충분히 주지 못할 경우 원본과 달라진다.(퀀타이징 효과)

8bit * 8kHz = 64000 bit per sec