Kwak Jisub

정리를 미루지 말자!

새싹 AI 프로그래머
화이팅!

4 분 소요

신호처리의 기초

파형의 종류

  • sin, cos: 정현파(sinusoidal signal)

임펄스(Impulse)

순간적인 충격을 말한다.
음성 시스템의 상태를 파악할 때 중요하다. -> 순간적인 충격으로 상태의 변화를 봄

In [1]: 
import numpy as np
import matplotlib.pyplot as plt
In [2]: 
X_analog = np.linspace(0, 2*np.pi, 1000)
y_analog = np.zeros(1000)
y_analog[500] = 1 # 임펄스: 순간적으로 무한대의 힘으로 충격을 가함

plt.plot(X_analog, y_analog)
plt.show()
Out [2]:

img

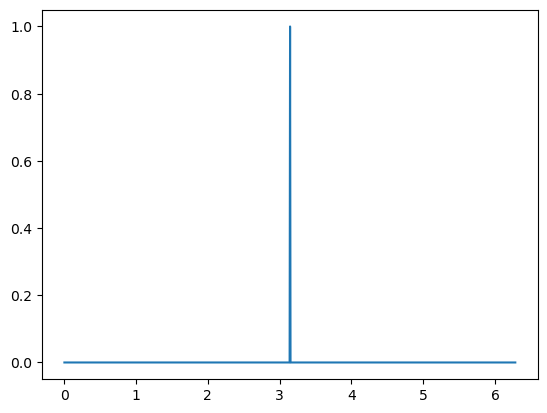
unit function

소리가 없다가 가해진 충격이 지속된다.

In [3]: 
X_analog = np.linspace(0, 2*np.pi, 1000)
y_analog = np.zeros(1000)
y_analog[500:] = 1 # 가해진 충격이 이후로도 지속됨

plt.plot(X_analog, y_analog)
plt.show()
Out [3]:

img

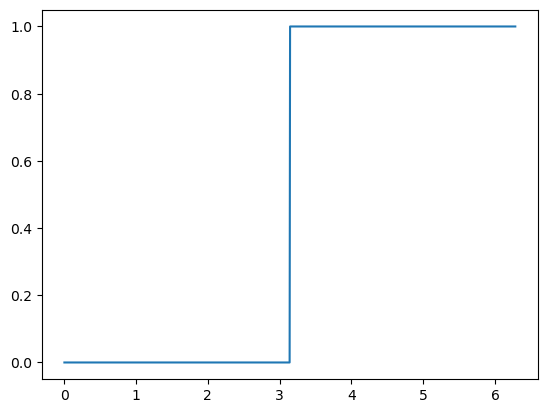
exponential function

소리가 기하급수적으로 증가한다.

In [4]: 
X_analog = np.linspace(0, 2*np.pi, 1000)
y_analog = np.ones(1000)
y_analog = y_analog * np.exp(X_analog)

plt.plot(X_analog, y_analog)
plt.show()
Out [4]:

img

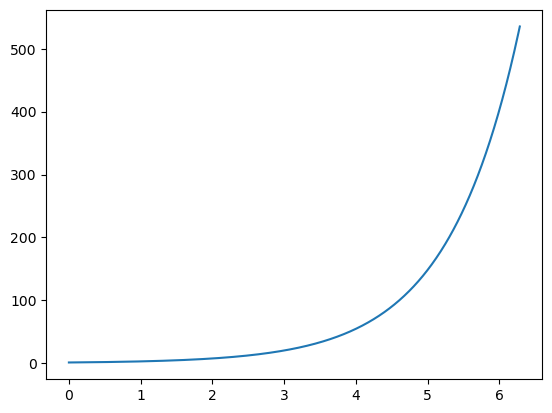
  • exponential(지수) function
    소리가 기하급수적으로 감소한다.(fadeout)
In [5]: 
X_analog = np.linspace(0, 2*np.pi, 1000)
y_analog = np.ones(1000)
y_analog = y_analog * np.exp(-X_analog) # fadeout

plt.plot(X_analog, y_analog)
plt.show()
Out [5]:

img

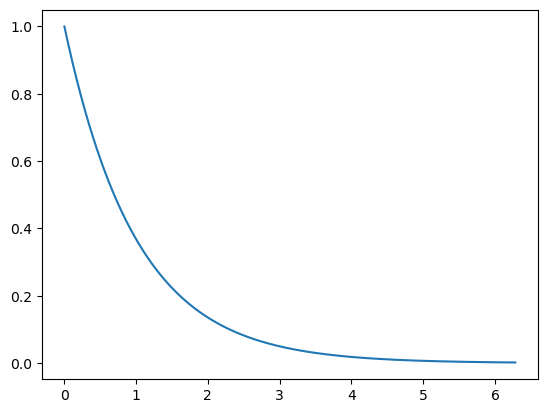
주파수

In [6]: 
X_digital = np.linspace(0, 2*np.pi, 50) # 한 주기가 1초라 가정하면
y_digital = np.sin(X_digital) # 1초 1주기
y_digital2 = np.sin(X_digital*2)# 1초 2주기
y_digital3 = np.sin(X_digital*3)# 1초 2주기, 주파수3Hz

plt.plot(X_digital, y_digital, 'o-')
plt.plot(X_digital, y_digital2, 'o-')
plt.plot(X_digital, y_digital3, 'o-')
plt.legend(['digital', 'digital_2', 'digital_3'])
plt.show()
Out [6]:

img

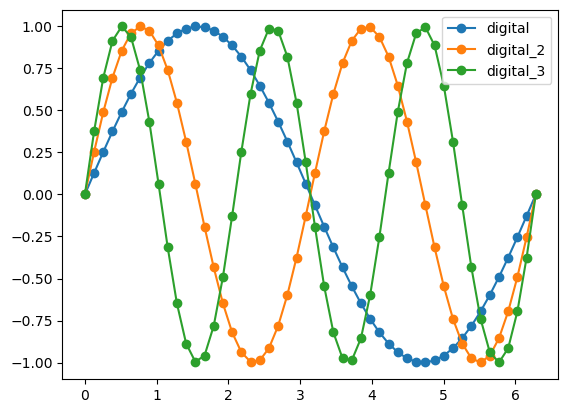
  • 주파수
    • 전파: 89.1MHz kbs2 fm 89100000Hz
    • 음역대: 4옥타브’라’음 440Hz ~ 8000Hz ~ 13000Hz

  • 진동수, 주파수, f(frequency), 단위:Hz
    샘플링 주파수 fs: 샘플링을 얼마나 자주했나

  • 샘플링 주파수가 중요한 이유
    1초 신호를 하나는 초당 8000개 샘플링(fs8000) vs 하나는 초당 16000개 샘플링(fs16000)
    fs8000[0~7999]
    fs16000[0~15999]
    fs가 주어지지 않는다면 단위시간을 알 수 없다.
    물리적 단위 시간을 기준으로 복원 가능!
In [7]: 
fs = 100 # 샘플링 주파수(1초에 몇개의 신호)
dt = 1/fs # 샘플 간 시간(몇초마다 신호를 캐치 하는지)
N = 300 # 샘플 갯수(3초) 100개가 모여야 1초, 300개이므로 3초!
In [8]: 
t = np.arange(0, N) * dt # 0 ~ 3초 사이
In [9]: 
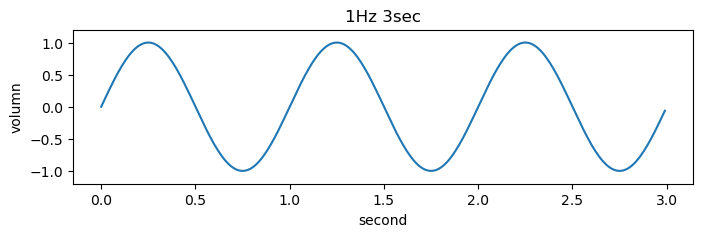
signal_1 = 1.0 * np.sin(2*np.pi * t) # 진폭(신호의 높낮이)을 가진 신호

plt.figure(figsize=(8, 2))
plt.plot(t, signal_1)
plt.title('1Hz 3sec')
plt.xlabel('second') # 시간
plt.ylabel('volumn') # 진폭
plt.ylim([-1.2, 1.2])
plt.show()
Out [9]:

img

In [10]: 
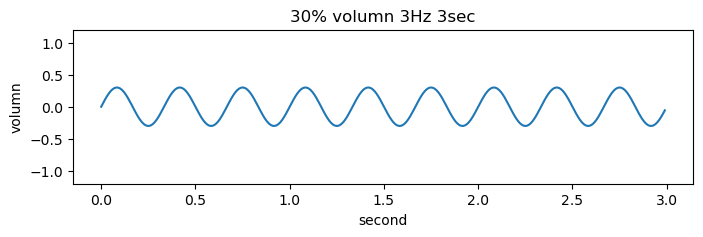
f = 3 # 주파수 3Hz
amp = 0.3 # 진폭
signal_2 = amp * np.sin(2*np.pi * f * t) # 기본 대비 3배 주파수(음높이 3배), 진폭 0.3배

plt.figure(figsize=(8, 2))
plt.plot(t, signal_2)
plt.title('30% volumn 3Hz 3sec')
plt.xlabel('second') # 시간
plt.ylabel('volumn') # 진폭
plt.ylim([-1.2, 1.2])
plt.show()
Out [10]:

img

In [11]: 
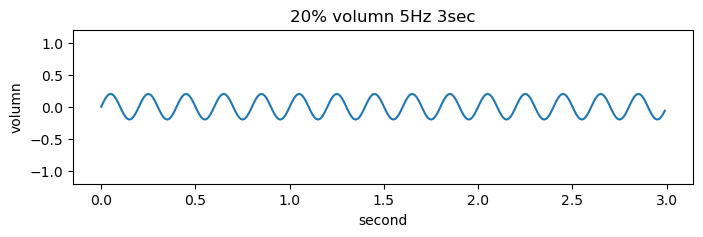
f = 5
amp = 0.2
signal_3 = amp * np.sin(2*np.pi * f * t)

plt.figure(figsize=(8, 2))
plt.plot(t, signal_3)
plt.title('20% volumn 5Hz 3sec')
plt.xlabel('second')
plt.ylabel('volumn')
plt.ylim([-1.2, 1.2])
plt.show()
Out [11]:

img

In [12]: 
plt.figure(figsize=(8, 4))
plt.plot(t, signal_1)
plt.plot(t, signal_2)
plt.plot(t, signal_3)
plt.legend(['100% vol 1Hz 3sec', '30% vol 3Hz 3sec', '20% vol 5Hz 3sec'])
plt.xlabel('second') # 시간
plt.ylabel('volumn') # 진폭
plt.ylim([-1.2, 1.2])
plt.show()
Out [12]:

img

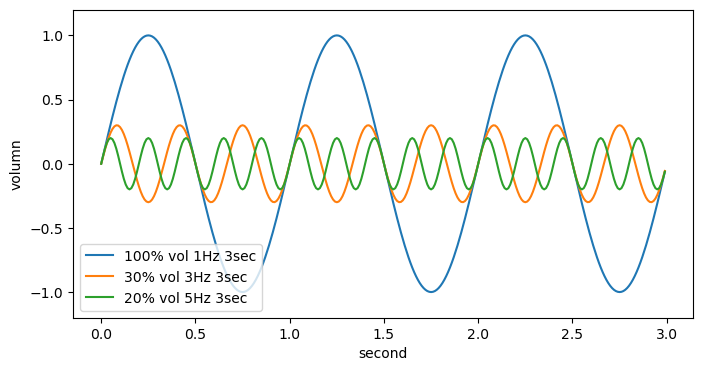
  • 실제 귀에 들리는 파형
In [13]: 
plt.figure(figsize=(8, 4))
plt.plot(t, signal_1+signal_2+signal_3)
plt.legend(['100% vol 1Hz 3sec + 30% vol 3Hz 3sec + 20% vol 5Hz 3sec'])
plt.xlabel('second') # 시간
plt.ylabel('volumn') # 진폭
plt.ylim([-1.2, 1.2])
plt.show()
Out [13]:

img

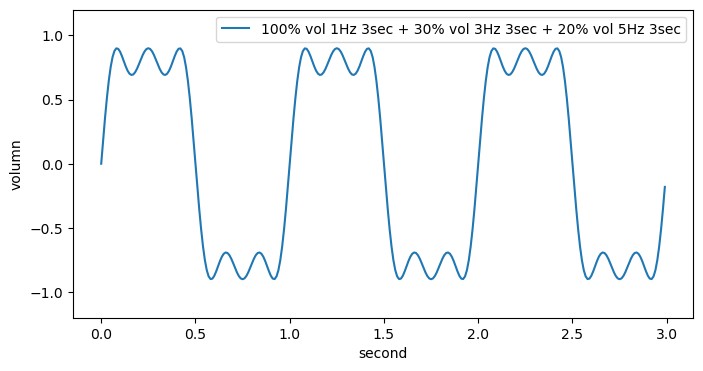
파형 분석

In [14]: 
df = fs / N # 주파수 간격
f = np.arange(0, N)
signals = signal_1 + signal_2 + signal_3
Xf = np.fft.fft(signals) # fft: 주파수 분석툴 -> 복소수
plt.subplot(121)
plt.plot(f, np.abs(Xf), 'o') # abs절대값
plt.subplot(122)
plt.plot(f[:N//2], np.abs(Xf[:N//2]), 'o')
plt.show()
Out [14]:

img

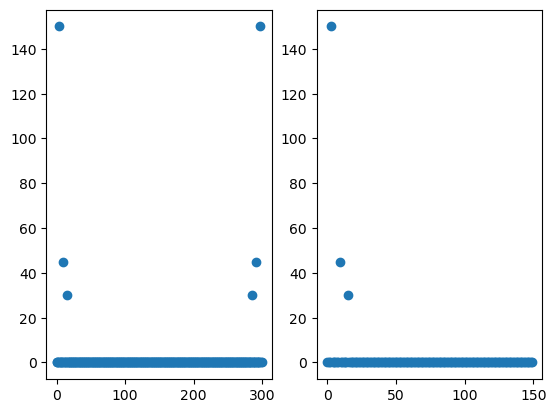
1Hz, 3Hz, 5Hz가 있다.
대칭구조에 반만 쓰면 된다.

In [15]: 
Xf[:5] # 복소수
Out [15]: 
array([-9.49612074e-16+0.00000000e+00j, -6.49443331e-15-2.33146835e-15j,
        2.45253753e-14+1.11465716e-15j, -2.30463730e-14-1.50000000e+02j,
        2.72803434e-14-1.96798384e-15j])

MFCC(Mel-Frequency Cepstral Coefficient)에서는 주파수당 출력값을 색깔로 표현한다.

나이퀴스트 샘플링 이론

Nyquist sampling theory

샘플링 레이트를 어떻게 가져가야 하는지에 대한 이론
fs는 적어도 f보다 2배 이상이어야 한다.(수식을 기반으로 유도)

실제 현업에서 틀린 말은 아니지만 10배 이상을 써야 이상한 상황을 피할 수 있다!

In [16]: 
# 원본
f = 20 # Hz
t = np.linspace(0, 0.5, 200)
x1 = np.sin(2.0*np.pi*f*t)

# 샘플링
fs = 35 # Hz (35개만 샘플링)
T = 1/fs
n = np.arange(0, 0.5/T)
nT = n*T
x2 = np.sin(2.0*np.pi*f*nT)
In [17]: 
plt.subplot(221)
plt.plot(t, x1)

plt.subplot(222)
plt.plot(t, x1) # 원본
plt.plot(nT, x2, 'o') # 디지털(샘플링 데이터)

plt.subplot(223)
plt.plot(t, x1) # 원본
plt.plot(nT, x2, 'o-') # 원본과 달라짐!
plt.show()
Out [17]:

img

In [18]: 
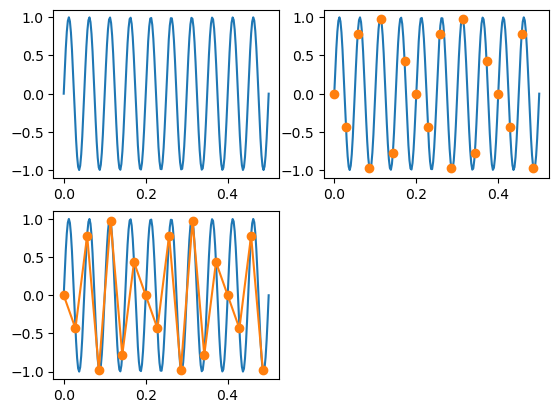
def nq_sampling(fs):
    f = 20 # Hz
    t = np.linspace(0, 0.5, 200)
    x1 = np.sin(2.0*np.pi*f*t)

    T = 1/fs
    n = np.arange(0, 0.5/T)
    nT = n*T
    x2 = np.sin(2.0*np.pi*f*nT)

    plt.subplot(221)
    plt.plot(t, x1)

    plt.subplot(222)
    plt.plot(t, x1)
    plt.plot(nT, x2, 'o')

    plt.subplot(223)
    plt.plot(t, x1)
    plt.plot(nT, x2, 'o-')
    plt.show()
  • 40개 샘플링
In [19]: 
nq_sampling(40)
Out [19]:

img

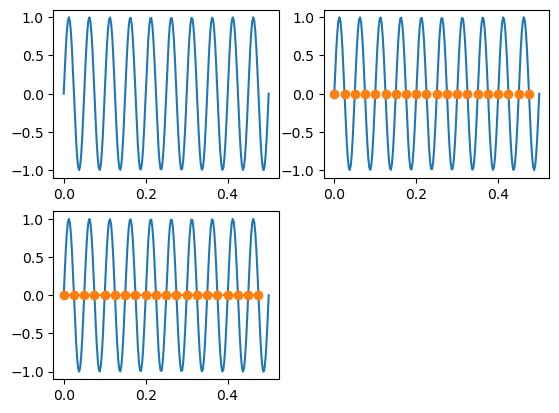
  • 41개 샘플링
In [20]: 
nq_sampling(41)
Out [20]:

img

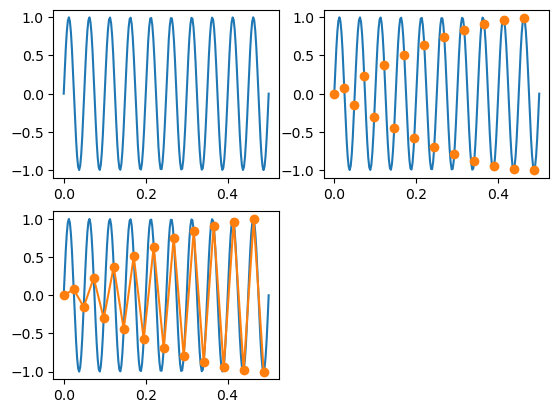
  • 45개 샘플링
In [21]: 
nq_sampling(45)
Out [21]:

img

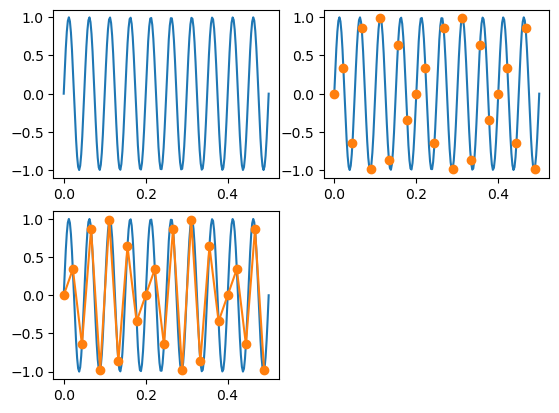
20의 2배를 넘는 45를 했지만 35와 차이가 없음

In [22]: 
nq_sampling(60)
Out [22]:

img

In [23]: 
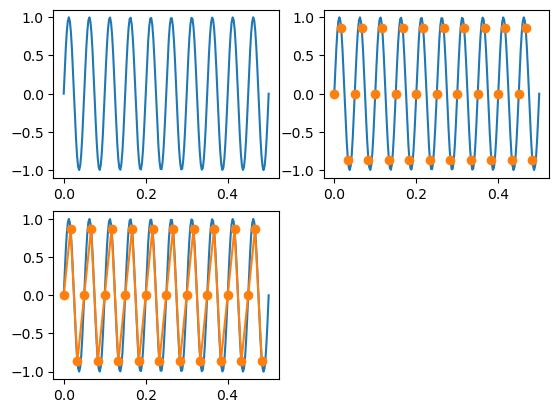
nq_sampling(405)
Out [23]:

img

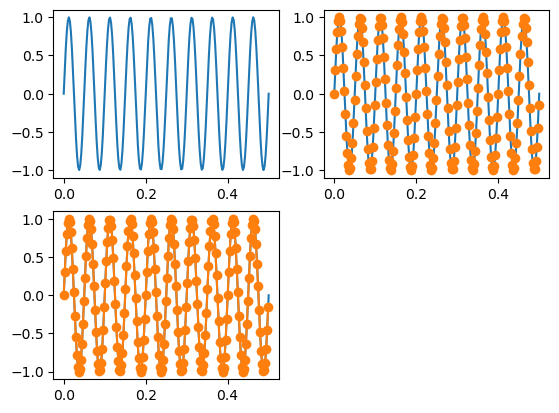
다양한 파형

In [24]: 
# 주파수(f)를 바꿔가며 파형 쌓기
fs = 100
dt = 1/fs
N = 300
t = np.arange(0, N) * dt

signals = 0
amp = 1
for f in range(1, 21):
    signals += amp * np.sin(2*np.pi * f * t)

plt.figure(figsize=(8, 2))
plt.plot(t, signals)
plt.xlabel('second')
plt.ylabel('volumn')
plt.show()
Out [24]:

img

In [25]: 
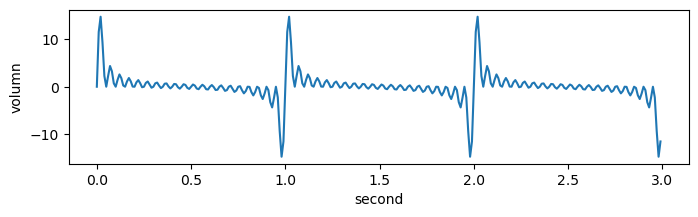
# 위에서 합친 파형 구현
fs = 100
dt = 1/fs
N = 300

t = np.arange(0, N) * dt

signals = 0
amps = [1, 0, 0.3, 0, 0.2, 0, 0, 0, 0, 0]
for f, amp in enumerate(amps):
    signals += amp * np.sin(2*np.pi * (f+1) * t)

plt.figure(figsize=(8, 2))
plt.plot(t, signals)
plt.xlabel('second')
plt.ylabel('volumn')
plt.show()
Out [25]:

img

In [26]: 
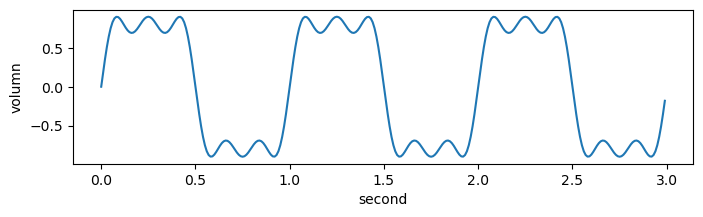
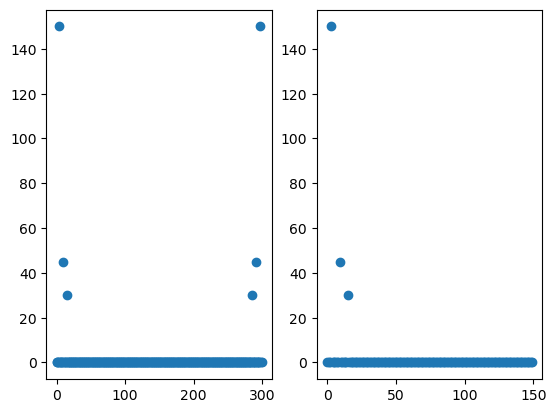
df = fs / N # 주파수 간격
f = np.arange(0, N)

Xf = np.fft.fft(signals) # fft: 주파수 분석툴 -> 복소수
plt.subplot(121)
plt.plot(f, np.abs(Xf), 'o')
plt.subplot(122)
plt.plot(f[:N//2], np.abs(Xf[:N//2]), 'o')
plt.show()
Out [26]:

img

  • bank 프리셋(주파수 성분)
    코드의 amps
In [27]: 
fs = 100
dt = 1/fs
N = 300

t = np.arange(0, N) * dt

signals2 = 0
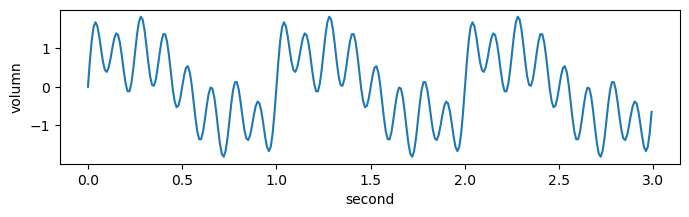
amps = [1, 0.1, 0.3, 0.3, 0.2, 0, 0, 0.8, 0, 0]
for f, amp in enumerate(amps):
    signals2 += amp * np.sin(2*np.pi * (f+1) * t)

plt.figure(figsize=(8, 2))
plt.plot(t, signals2)
plt.xlabel('second')
plt.ylabel('volumn')
plt.show()
Out [27]:

img

In [28]: 
df = fs / N # 주파수 간격
f = np.arange(0, N)

Xf = np.fft.fft(signals2) # fft: 주파수 분석툴 -> 복소수
plt.subplot(121)
plt.plot(f, np.abs(Xf), 'o')
plt.subplot(122)
plt.plot(f[:N//2], np.abs(Xf[:N//2]), 'o')
plt.show()
Out [28]:

img

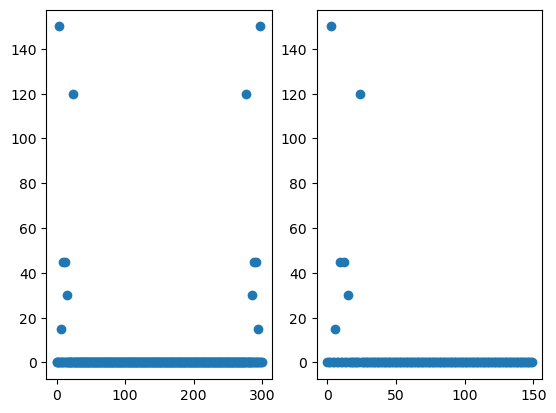
  • 하모닉스
In [29]: 
def freq_amps(amps):
    fs = 100
    dt = 1/fs
    N = 300

    t = np.arange(0, N) * dt

    signals2 = 0
    for f, amp in enumerate(amps):
        signals2 += amp * np.sin(2*np.pi * (f+1) * t)

    plt.figure(figsize=(8, 2))
    plt.plot(t, signals2)
    plt.xlabel('second')
    plt.ylabel('volumn')
    plt.show()
In [30]: 
amps = [0, 1, 0, 0.2, 0, 0, 0, 0.3, 0, 0] # 하모닉스: 배음(실제 악기, 자연현상), 기본 sin형태로는 나타나지 않고 배수의 주파수에 약한 파형이 나타남
freq_amps(amps)
Out [30]:

img

In [31]: 
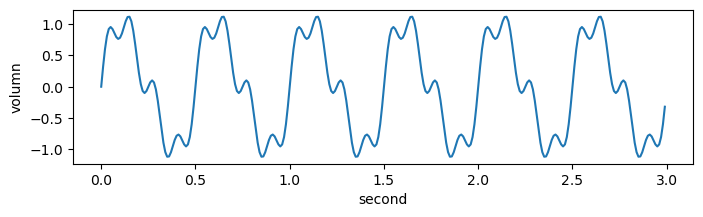
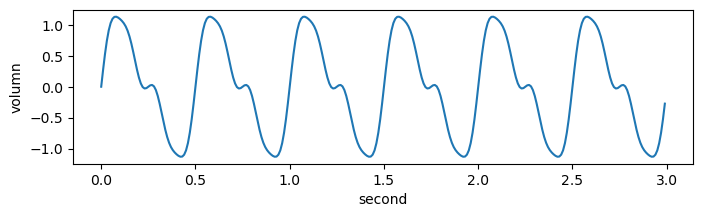
amps = [0, 1, 0, 0.4, 0, 0, 0, 0.1, 0, 0] # 하모닉스: 배음(같은 악기라도 다른 형태;다른 파형;다른 질감)
freq_amps(amps)
Out [31]:

img

댓글남기기

참고